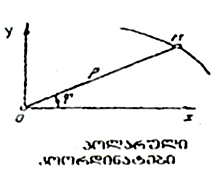
კოორდინატები პოლარული

კოორდინატები პოლარული – ორი სიდიდე ρ და φ, რომლებიც შემდეგნაირად განსაზღვრავენ წერტილის მდებარეობას სიბრტყეზე: სიბრტყეზე აღებულია რაიმე 0 წერტილი (პოლუსი) და სხივი (პოლარული ღერძი), სათავით 0 წერტილში. სიბრტყის ნებისმიერ M წერტილს შეესაბამება ორი რიცხვი: p - პოლარული რადიუსი, რომელიც 0M მონაკვეთის სიგრძის ტოლია, და φ - პოლარული კუთხე, რომელიც პოლარულ ღერძსა და 0M სხივს შორის კუთხის ტოლია; ამასთანავე, 0≤ρ<∞; 0≤φ<2π (ზოგჯერ 0≤φ <2πk).

თუ სიბრტყეზე ავიღებთ დეკარტის მართკუთხა კოორდინატთა 0xy სისტემას ისე, რომ 0 სათავე დაემთხვეს პოლუსს, ხოლო 0x ღერძი - პოლარულ ღერძს, მაშინ M წერტილის დეკარტის კოორდინატებსა და პოლარულ კოორდინატებს შორის დამოკიდებულება გამოისახება ფორმულებით:

x = p cosφ; y=psinφ. p = tgφ = y/x, x ≠ 0.

მანძილი M₁ (p₁, φ₁) და M₂ (p₂, φ₂) წერტილებს შორის:

სამკუთხედის ფართობი M₁ (p₁ φ₁), M₂ (p₂, φ₂) და M₃ (p₃, φ₃) წვეროებით:

S = [p₁ p₂ sin⁡(φ₂-φ₁ ) + p₂ p₃ sin(φ₃-φ₂) + p₃ p₁ sin⁡(φ₁-φ₃)].

კერძოთ, თუ p₃ = 0, მაშინ

S = [p₁ p₂ sin⁡(φ₂ - φ₁)]

პოლარულ კოორდინატებს დიდი ხნის ისტორია აქვს. ჯერ კიდევ IV საუკუნეში ჩვ. წ.აღ-მდე დინოსტრატი იკვლევდა კვადრატრისას, რომლის განტოლება პოლარულ კოორდინატებში ასე ჩაიწერება: p=2r/π∙φ/Sinφ; პოლარული კოორდინატების მსგავსი გამოიყენა დიურერმა, რომელიც აგებდა არქიმედეს ხვიას, კარდიოიდის ერთ სახეს, ლოგარითმულ ხვიას და სხვ. (1525). პოლარული კოორდინატებით სარგებლობდა ნიუტონიც; ნაშრომში „ფლუქსიის მეთოდი“ იგი სამჯერ სარგებლობს პოლარული კოორდინატებით და მოჰყავს ფორმულები, რომლებიც აკავშირებენ პოლარულ და მართკუთხა კოორდინატებს შემდეგი სახით: xx + yy = tt, tv =y, სადაც t – რადიუს-ვექტორია, ხოლო v = siny.

თითქმის თანამედროვე სახით პოლარული კოორდინატები გვხვდება იაკობ ბერნულისთან (1891): წერტილის კოორდინატებად მან აიღო წრეწირის რკალის სიგრძე (თანამედროვე φ კუთხე) და ამ წრეწირისადმი პერპენდიკულარების სიგრძე (თანამედროვე p). მხოლოდ ეილერის შრომებში გამოჩნდა ფორმულები x = p cosφ; y = psiφ, (1748).

გამოთქმა „პოლარული განტოლება“ შემოიღო ფონტანამ (1784), ხოლო სახელწოდება „პოლარული კოორდინატები“ შემოიღეს XIX საუკუნეში. სიტყვა „პოლუსი“ დაფუძნდა მონჟისა და მისი სკოლის შრომების შემდეგ (1802).

სახელწოდება „პოლარული ღერძი“ შემოიღო მაგნუსმა (1833). პოლარულმა φ კუთხემ ვერ მიიღო სახელწოდება XIX საუკუნეში; მას უწოდებდნენ „ანომალიას“, „ამპლიტუდას“, „აზიმუტს“ ან „არგუმენტს“.

1857 წელს გამოვიდა გრუნერტის სახელმძღვანელო, სადაც მთელი გეომეტრია, დიფერენციალური გეომეტრიის ჩათვლით, დაფუძნებულია პოლარულ კოორდინატთა სისტემის გამოყენებაზე. თანამედროვე აღნიშვნებთან ყველაზე უფრო ახლოს არის ეილერის (z და φ) და გურიევის (r და ω) აღნიშვნები.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი