რგოლი (მათემატიკა)
NPLG Wiki Dictionaries გვერდიდან
(სხვაობა ვერსიებს შორის)
(ახალი გვერდი: '''რგოლი''' '''რგოლი''' 1. სიბრტყის წერტილთა სიმრავლე...) |
|||
| ხაზი 1: | ხაზი 1: | ||
[[ფაილი:Rgoli.PNG|thumb|'''რგოლი''']] | [[ფაილი:Rgoli.PNG|thumb|'''რგოლი''']] | ||
| − | '''რგოლი''' | + | '''რგოლი''' − ტერმინი Ring – „რგოლი“, „სარტყელი“ შემოთავაზებულია ჰილბერტის მიერ. |
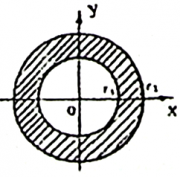
| − | 1. სიბრტყის წერტილთა სიმრავლე, რომელიც შემოსაზღვრულია ორი კონცენტრული წრეწირით და შეიცავს ამ წრეწირებს. | + | 1. [[სიბრტყე (გეომეტრია)|სიბრტყის]] [[წერტილი (გეომეტრია)|წერტილთა]] [[სიმრავლე]], რომელიც შემოსაზღვრულია ორი [[კონცენტრული წრეწირები|კონცენტრული წრეწირით]] და შეიცავს ამ [[წრეწირი|წრეწირებს]]. |
| − | 2. არაცარიელი R სიმრავლე, რომელშიც განსაზღვრულია ორი ოპერაცია – შეკრება და გამრავლება. ეს ოპერაციები R-ის განსაზღვრული რიგით აღებულ ნებისმიერ ორ a და b ელემენტს უთანადებენ შესაბამისად ერთ ელემენტს – ჯამს (a+b) -ს R-დან და ერთ ელემენტს – ნამრავლს (a∙b) -ს R-დან. ამასთანავე, სრულდება შემდეგი პირობები: | + | 2. არაცარიელი R სიმრავლე, რომელშიც განსაზღვრულია ორი ოპერაცია – [[შეკრება (არითმეტიკა)|შეკრება]] და [[გამრავლება]]. ეს ოპერაციები R-ის განსაზღვრული რიგით აღებულ ნებისმიერ ორ a და b [[ელემენტი (მათემატიკა)|ელემენტს]] უთანადებენ შესაბამისად ერთ ელემენტს – [[ჯამი (მათემატიკა)|ჯამს]] (a+b) -ს R-დან და ერთ ელემენტს – [[ნამრავლი|ნამრავლს]] (a∙b) -ს R-დან. ამასთანავე, სრულდება შემდეგი [[პირობა (მათემატიკა)|პირობები]]: |
| − | :1) a+b = b+a – შეკრების კომუტატიურობა; | + | :1) a+b = b+a – შეკრების [[კომუტატიურობა]]; |
| − | :2) a+(b+c) =(a+b)+c – შეკრების ასოციაციურობა; | + | :2) a+(b+c) =(a+b)+c – შეკრების [[ასოციაციურობა]]; |
| − | :3) ნებისმიერ a და b -თვის a+x = b | + | :3) ნებისმიერ a და b -თვის a+x = b [[განტოლება]]ს აქვს ერთადერთი ამონახსნი: x = b-a; |
| − | :4) a(b+c) = ab+ac; (b+c)a = ba+ca – გამრავლების დისტრიბუციულობა. | + | :4) a(b+c) = ab+ac; (b+c)a = ba+ca – გამრავლების [[დისტრიბუციულობა]]. |
| − | რგოლის ცნება შემოიღო დედეკინდმა, ამასთანავე, იგი რგოლს უწოდებდა „რიგობითს“ | + | რგოლის ცნება შემოიღო დედეკინდმა, ამასთანავე, იგი რგოლს უწოდებდა „რიგობითს“. |
16:53, 9 ოქტომბერი 2023-ის ვერსია
რგოლი − ტერმინი Ring – „რგოლი“, „სარტყელი“ შემოთავაზებულია ჰილბერტის მიერ.
1. სიბრტყის წერტილთა სიმრავლე, რომელიც შემოსაზღვრულია ორი კონცენტრული წრეწირით და შეიცავს ამ წრეწირებს.
2. არაცარიელი R სიმრავლე, რომელშიც განსაზღვრულია ორი ოპერაცია – შეკრება და გამრავლება. ეს ოპერაციები R-ის განსაზღვრული რიგით აღებულ ნებისმიერ ორ a და b ელემენტს უთანადებენ შესაბამისად ერთ ელემენტს – ჯამს (a+b) -ს R-დან და ერთ ელემენტს – ნამრავლს (a∙b) -ს R-დან. ამასთანავე, სრულდება შემდეგი პირობები:
- 1) a+b = b+a – შეკრების კომუტატიურობა;
- 2) a+(b+c) =(a+b)+c – შეკრების ასოციაციურობა;
- 3) ნებისმიერ a და b -თვის a+x = b განტოლებას აქვს ერთადერთი ამონახსნი: x = b-a;
- 4) a(b+c) = ab+ac; (b+c)a = ba+ca – გამრავლების დისტრიბუციულობა.
რგოლის ცნება შემოიღო დედეკინდმა, ამასთანავე, იგი რგოლს უწოდებდა „რიგობითს“.