პარალელეპიპედი
(ახალი გვერდი: '''პარალელეპიპედი''' – პრიზმა, რომელსაც ფუძედ აქვს პარალელოგრ...) |
|||
| ხაზი 1: | ხაზი 1: | ||
'''პარალელეპიპედი''' – პრიზმა, რომელსაც ფუძედ აქვს პარალელოგრაში. ტერმინი ბერძნულია παραλληλοζ – პარალელური და επιπεδοζ – სიბრტყე, ზედაპირი. ეს ტერმინი გვხვდება ევკლიდესთან, ჰერონთან. არქიმედესთან ეს ტერმინი არ გვხვდება. | '''პარალელეპიპედი''' – პრიზმა, რომელსაც ფუძედ აქვს პარალელოგრაში. ტერმინი ბერძნულია παραλληλοζ – პარალელური და επιπεδοζ – სიბრტყე, ზედაპირი. ეს ტერმინი გვხვდება ევკლიდესთან, ჰერონთან. არქიმედესთან ეს ტერმინი არ გვხვდება. | ||
| − | + | [[ფაილი:Paralelepipedi.PNG|მარჯვნივ|200პქ]] | |
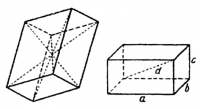
პარალელეპიპედის წახნაგები წყვილ-წყვილად ტოლი პარალელოგრამებია. პარალელეპიპედს აქვს 6 წახნაგი, 8 წვერო, 12 წიბო. თუ გვერდითი წახნაგები ფუძის პერპენდიკულარულია, მაშინ პარალელეპიპედს ეწოდება მართი. თუ, ამასთანავე, ფუძე მართკუთხედია, მაშინ პარალელეპიპედს მართკუთხას უწოდებენ. მართკუთხა პარალელეპიპედში ყველა დიაგონალი ერთმანეთის ტოლია. თუ a, b, c მართკუთხა პარალელეპიპედის გვერდებია, ხოლო d – დიაგონალი, მაშინ d<sup>2</sup> = a<sup>2</sup>+ b<sup>2</sup> + c<sup>2</sup>. | პარალელეპიპედის წახნაგები წყვილ-წყვილად ტოლი პარალელოგრამებია. პარალელეპიპედს აქვს 6 წახნაგი, 8 წვერო, 12 წიბო. თუ გვერდითი წახნაგები ფუძის პერპენდიკულარულია, მაშინ პარალელეპიპედს ეწოდება მართი. თუ, ამასთანავე, ფუძე მართკუთხედია, მაშინ პარალელეპიპედს მართკუთხას უწოდებენ. მართკუთხა პარალელეპიპედში ყველა დიაგონალი ერთმანეთის ტოლია. თუ a, b, c მართკუთხა პარალელეპიპედის გვერდებია, ხოლო d – დიაგონალი, მაშინ d<sup>2</sup> = a<sup>2</sup>+ b<sup>2</sup> + c<sup>2</sup>. | ||
მიმდინარე ცვლილება 16:41, 26 ოქტომბერი 2023 მდგომარეობით
პარალელეპიპედი – პრიზმა, რომელსაც ფუძედ აქვს პარალელოგრაში. ტერმინი ბერძნულია παραλληλοζ – პარალელური და επιπεδοζ – სიბრტყე, ზედაპირი. ეს ტერმინი გვხვდება ევკლიდესთან, ჰერონთან. არქიმედესთან ეს ტერმინი არ გვხვდება.
პარალელეპიპედის წახნაგები წყვილ-წყვილად ტოლი პარალელოგრამებია. პარალელეპიპედს აქვს 6 წახნაგი, 8 წვერო, 12 წიბო. თუ გვერდითი წახნაგები ფუძის პერპენდიკულარულია, მაშინ პარალელეპიპედს ეწოდება მართი. თუ, ამასთანავე, ფუძე მართკუთხედია, მაშინ პარალელეპიპედს მართკუთხას უწოდებენ. მართკუთხა პარალელეპიპედში ყველა დიაგონალი ერთმანეთის ტოლია. თუ a, b, c მართკუთხა პარალელეპიპედის გვერდებია, ხოლო d – დიაგონალი, მაშინ d2 = a2+ b2 + c2.
ზედაპირის სრული ფართობი S=2(ab+bc+ac); მოცულობა V=abc. თუ პარალელეპიპედის ყოველი წახნაგი კვადრატია, მაშინ პარალელეპიპედს ეწოდება კუბი. მართკუთხა პარალელეპიპედის ერთი წვეროდან გამომავალ სამივე წიბოს სიგრძეს პარალელეპიპედის განზომილებებს უწოდებენ. ყოველ პარალელეპიპედს აქვს სიმეტრიის ცენტრი – დიაგონალების გადაკვეთის წერტილი.