მოცულობა (გეომეტრია)
(ახალი გვერდი: '''მოცულობა''' – სამგანზომილებიანი არაუარყოფითი ადიტიური ფუნ...) |
|||
| ხაზი 13: | ხაზი 13: | ||
[[კატეგორია:მათემატიკა]] | [[კატეგორია:მათემატიკა]] | ||
| + | [[კატეგორია:გეომეტრია]] | ||
მიმდინარე ცვლილება 17:04, 14 ივნისი 2023 მდგომარეობით
მოცულობა – სამგანზომილებიანი არაუარყოფითი ადიტიური ფუნქცია, რომელიც არ იცვლის თავის მნიშვნელობას სხეულის მოძრაობის დროს. ეს არის გეომეტრიულ სხეულებთან დაკავშირებული ერთ-ერთი ძირითადი სიდიდე. უმარტივეს შემთხვევაში მოცულობა იზომება ერთეული სიგრძის წიბოების მქონე იმ კუბების რაოდენობით, რომლებიც მოცემულ სხეულში ეტევა.
პრაქტიკული მოთხოვნილებებიდან გამომდინარე, უმარტივესი სხეულების მოცულობის გამოთვლის ამოცანა გეომეტრიის განვითარების ერთ-ერთი სტიმული იყო ძველი აღმოსავლეთის (ბაბილონი, ეგვიპტე) მათემატიკოსები ფლობდნენ მოცულობის გამოთვლის ზოგიერთ წესს ისეთი სხეულებისათვის, რომლებიც ყველაზე უფრო ხშირად გვხვდება პრაქტიკაში (პრიზმული ძელები, სრული და წაკვეთილი პირამიდები, ცილინდრები და სხვ.). ეს იყო სხეულის მოცულობის მიახლოებითი – ემპირიული გამოთვლის ხერხები. მოცულობის გამოთვლის თეორია მიახლოებითი წესებისაგან გაათავისუფლეს ბერძენმა მათემატიკოსებმა; ევკლიდეს „საწყისებში“ და არქიმედეს თხზულებებში არის მრავალწახნაგებისა და ზოგიერთი მრგვალი სხეულის (ცილინდრის, კონუსის, სფეროს და მათი ნაწილების) მოცულობის გამოსათვლელი ზუსტი ფორმულები. მოცულობის გამოთვლის თანამედროვე თეორიის საფუძველია ზღვართა თეორია და ინტეგრალური აღრიცხვა.
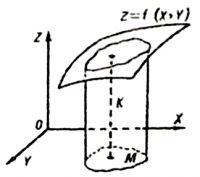
ანალიზურად მოცულობა შეიძლება გამოისახოს ორჯერადი ინტეგრალის საშუალებით. ვთქვათ, K სხეული შემოსაზღვრულია 0z ღერძის პარალელური მსახველების მქონე ცილინდრული ზედაპირით, Oxy სიბრტყის M კვადრირებადი არითა და f(x,y) ზედაპირით, რომელსაც ცილინდრის მსახველის ნებისმიერი პარალელი კვეთს ერთსა და მხოლოდ ერთ წერტილში. ასეთი სხეულის მოცულობა შეიძლება გამოვთვალოთ ორჯერადი ინტეგრალით: