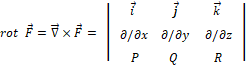ნაბლა ოპერატორი

ნაბლა ოპერატორი ( – ოპერატორი, ანუ ჰამილტონის ოპერატორი) – ველის თეორიის ძირითადი ცნება – დიფერენციალური ოპერატორი, რომელიც განსაზღვრულია სამი ცვლადის დიფერენცირებად ფუნქციებზე; სიმბოლურად ჩაიწერება ვექტორის სახით: = ∂/∂x + ∂/∂y + ∂/∂z , სადაც – დეკარტის x,y,z ღერძების დადებითი მიმართულების ერთეულოვანი ვექტორებია.

ევკლიდეს სამგანზომილებიან სივრცეში სკალარული და ვექტორული ველის დიფერენციალური მახასიათებლები მარტივად და ნათლად გამოისახებიან ნაბლა ოპერატორის საშუალებით. მაგალითად:

ა) სკალარული f(x,y,z) ველის გრადიენტი:

gradf = f =∂f/∂x + ∂f/∂y + ∂f/∂z ;

ბ) ფაილი:Nabla017.png = P + Q + R ვექტორული ველის დივერგენცია:

div ფაილი:Nabla017.png = = ∂P/∂x + ∂Q/∂y + ∂R/∂z ;

გ) იმავე ფაილი:Nabla017.png ვექტორის როტორი:

აქ, ა) -ში f – გამოსახავს „ვექტორის ნამრავლს რიცხვზე“, ბ) -ში – „ორი ვექტორის სკალარულ ნამრავლს“, გ) -ში – „ორი ვექტორის ვექტორულ ნამრავლს“, იმ განსხვავებით, რომ ∂/∂x,∂/∂y,∂/∂z -ის ნამრავლი რაიმე ფუნქციაზე აღნიშნავს ამ ფუნქციის წარმოებულს შესაბამისი არგუმენტით. ამ ანალოგიის მოხერხებულობა შემდეგი გამოთვლებიდანაც ჩანს:

div gradf=∇ ⃗∙∇ ⃗f=∇ ⃗^2 f,

grad div F ⃗=∇ ⃗•(∇ ⃗•F ⃗)=∇ ⃗^2 F ⃗+∇ ⃗×(∇ ⃗×F ⃗),

rot rot F ⃗=∇ ⃗ ×(∇ ⃗×F ⃗ )=∇ ⃗•∇ ⃗ F ⃗- ∇ ⃗^2 F ⃗

rot gradf=∇ ⃗×∇ ⃗ f=0 ;

div rot F ⃗=∇ ⃗∙(∇ ⃗×F ⃗ )=0.

აქ ∇ ⃗^2 f ≡ ∂^2 f/∂x^2 + ∂^2 f/∂y^2+∂^2 f/∂z^2,

∇ ⃗^2 F ⃗≡∇ ⃗^2 F_x i ̇ ⃗+∇ ⃗^2 F_y j ̇ ⃗+∇ ⃗^2 F_z k ⃗ .

ნაბლა ოპერატორი შემოიღო ჰამილტონმა (1853). მან იგი აღნიშნა ∇ ⃗ სიმბოლოთი და არავითარი სახელი არ უწოდებია. ამ ოპერატორს იგი იყენებდა მხოლოდ ფუნქციისათვის. ის ფაქტი, რომ ∇ ⃗ ოპერატორის საშუალებით შეიძლება გამოისახოს დივერგენცია, როტორი და გრადიენტი, აღმოაჩინა თეტმა (1862).

ამ ოპერატორს ჰევისაიდი დასაწყისში უწოდებდა „ჰამილტონის ოპერატორს“, ხოლო 1892 წლიდან მას უწოდა „ნაბლა“, რადგანაც სიმბოლო ∇ წარმოადგენს ფინიკიელების ალფაბეტის ასოს, რომელიც ძალიან წააგავს ასურულ მუსიკალურ ინსტრუმენტს – ქნარს (არფას), ქნარს კი ბერძნულად ეწოდება ναβλα. სანამ ეს ტერმინი დაფუძნდებოდა, მრავალი ავტორი ამ ოპერატორს უწოდებდა atled-ს, რომელიც მიიღება „delta“-ს უკუღმა წაკითხვით.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი