ციკლოიდი
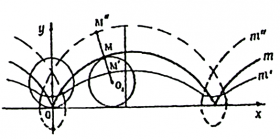
ციკლოიდი – ბრტყელი წირი, რომელსაც შემოწერს r რადიუსის წრესთან უძრავად დაკავშირებული ფიქსირებული M წერტილი, როდესაც ეს წრე უსრიალოდ მიგორავს უძრავ წრფეზე.
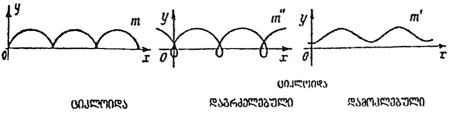
თუ M წერტილი მდებარეობს წრეწირზე, მივიღებთ ჩვეულებრივ ციკლოიდს (m), თუ წრის შიგნით – დამოკლებულ ციკლოიდს (m'), თუ წრის გარეთ – დაგრძელებულ ციკლოიდს (m"). ორ უკანასკნელ წირს ტროქოიდებს უწოდებენ. ციკლოიდის პარამეტრული სახის განტოლება ასეთია:
- x = rt - asint, y=r - acost,
სადაც a არის მანძილი M წერტილიდან წრის ცენტრამდე, t - პარამეტრი, კუთხე, რომლითაც შემობრუნდა წრე (ან მისი რადიუსი) წრფეზე გორვისას. დეკარტის კოორდინატებში ციკლოიდის განტოლება ასე ჩაიწერება:
ციკლოიდი გამოიყენება ტექნიკაში და მექანიზმების თეორიაში.
სახელწოდება წარმოქმნილია ბერძნული სიტყვიდან kykloeides – წრისმაგვარი. kyklos – „წრე“, „წრეწირი“ და eides, რაც რთულ სიტყვაში ნიშნავს წარმოშობას, ასე, რომ, სიტყვა სიტყვით აზრი ტერმინისა არის – „წრის მიერ წარმოქმნილი“. ციკლოიდის აღმოჩენის ისტორია გაურკვეველია; ძველ დროში მას არ იცნობდნენ. როგორც ჩანს, იგი პირველად გვხვდება დე - ბუვილთან (1501) წრის კვადრატურის ამოცანასთან დაკავშირებით. სახელწოდება მას მიანიჭა გალილეიმ (1598), რომელმაც პირველმა დაიწყო ამ წირის შესწავლა. ერთგვაროვანი ფირფიტისაგან გამოჭრილი ფიგურების აწონვით მან განსაზღვრა, რომ ციკლოიდით შემოსაზღვრული ფართობი სამჯერ მეტია შესაბამისი წრის ფართობზე. ასეთი გზით გალილეის იმედი ჰქონდა ამოეხსნა წრის კვადრატურის ამოცანა.
შეიძლება ითქვას, რომ ციკლოიდის ისტორია იწყება 1628 წლიდან, როდესაც მ. მერსენმა, რომელმაც მისი განსაზღვრა შეიტყო, ალბათ, გალილეის მოწაფეებისაგან, მიაქცია მას მათემატიკოსების ყურადღება. ციკლოიდით შემოსაზღვრული ფართობი გამოთვალა გ. რობერვალმა (1634-1636). ეს შედეგი დაასაბუთეს ფერმამ და დეკარტმა (1638). 20 წლის შემდეგ ქ. რენმა მოახდინა ციკლოიდის გაწრფევება (1658). შემდგომში ციკლოიდს შეისწავლიდა თითქმის ყველა გამოჩენილი მათემატიკოსი (პასკალი, ჰიუგენსი, დეკარტი და სხვ.). ჰიუგენსმა დაადგინა, რომ ციკლოიდი არის ტაუტოქრონა, ი. ბერნულმა აჩვენა, რომ იგი ასევე არის ბრაქისტოქრონა.