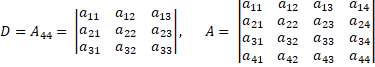ზედაპირები მეორე რიგის

ზედაპირები მეორე რიგის – ზედაპირები, რომელთა წერტილების დეკარტის მართკუთხა კოორდინატები x,y,z აკმაყოფილებენ მეორე ხარისხის ალგებრულ განტოლებას:

a₁₁x² + a₂₂y² + a₃₃z² + 2a₁₂xy + 2a₁₃xz + 2a₂₃ yz + 2a₁₄x + 2a₂₄y + 2a₃₄z + a₄₄ = 0. (*)

ან

(a₁₁x + a₁₂y + a₁₃z + a₁₄)x + (a₂₁x + a₂₂y + a₂₃z + a₂₄)y + (a₃₁x + a₃₂y + a₃₃z + a₃₄)z + (a₄₁x + a₄₂y + a₄₃z + a₄₄) = 0.

სადაც a_ik = a_ki; i,k = 1,2,3,4.

ნებისმიერი (*) განტოლებისათვის ოთხი სიდიდე I, J, D, A წარმოადგენს ინვარიანტულს კოორდინატთა ღერძების პარალელური გადატანის ან მობრუნების მიმართ:

აქ A₄₄ არის a₄₄ ელემენტის ალგებრული დამატება.

ეს ინვარიანტები განსაზღვრავენ ზედაპირების თვისებებს სივრცეში მათი მდებარეობისაგან დამოუკიდებლად. A დეტერმინანტს ეწოდება (*) განტოლების დისკრიმინანტი.

(*) განტოლება შეიძლება არ განსაზღვრავდეს ნამდვილ გეომეტრიულ სახეს; მაშინ იტყვიან, რომ იგი განსაზღვრავს წარმოსახვით მეორე რიგის ზედაპირს.

ამ განტოლებაში a_ik (i,k=1,2,3) კოეფიციენტები ყველა ერთდროულად არ არის ნულის ტოლი.

მეორე რიგის ზედაპირთა თეორიის ძირითადი ამოცანა მდგომარეობს ამ ზედაპირების კლასიფიკაციაში, მათი ინვარიანტების მოძებნაში, აგრეთვე სივრცეში კოორდინატთა იმ სისტემის დადგენაში, რომელშიც მოცემულ მეორე რიგის ზედაპირს აქვს უმარტივესი – კანონიკური განტოლება.

სულ არსებობს მეორე რიგის ზედაპირების 17 სხვადასხვა სახე (ევკლიდეს სივრცეში): ცილინდრები (ელიფსური ნამდვილი და წარმოსახვითი, პარაბოლური და ჰიპერბოლური), კონუსები (ნამდვილი და წარმოსახვითი), ელიფსოიდი (ნამდვილი ან წარმოსახვითი), ჰიპერბოლოიდი (ცალკალთა და ორკალთა), პარაბოლოიდი (ელიფსური და ჰიპერბოლური), ორი ნამდვილი გადამკვეთი სიბრტყე, ორი წარმოსახვითი სიბრტყე (რომლებიც იკვეთებიან ნამდვილ წრფეზე), ორი თანხვდენილი სიბრტყე. (იხ. „მეორე რიგის ზედაპირები“).

მეორე რიგის ზედაპირებს, რომლებსაც გააჩნიათ სიმეტრიის ცენტრი, ცენტრალური ზედაპირები ეწოდებათ.

მეორე რიგის ზედაპირები მეორე ხარისხის განტოლების სახით პირველად ლ. ეილერმა წარმოადგინა. მეორე რიგის გადაუგვარებელი ზედაპირების თანამედროვე სახელწოდებები გაჩნდა მხოლოდ XIX საუკუნის დასაწყისში გ. მონჟის წიგნში (1801). მონჟის სახელწოდებებს ცხადად ამჩნევიათ ეილერის ტერმინოლოგიის კვალი: ეილერთან – „ელიპტოიდი“, მონჟთან – „ელიფსოიდი“, ასევე „ელიპტიკურ-პარაბოლური ზედაპირი“ და „ელიფსური პარაბოლოიდი“ და ა.შ. (მანამდე „პარაბოლოიდი“ და „ჰიპერბოლოიდი“ ნიშნავდა მაღალი რიგის პარაბოლას და ჰიპერბოლას).

დაწყებული ლ. ეილერის შრომიდან „უსასრულოდ მცირეთა ანალიზის შესავალი“ (1748) ზედაპირთა კლასიფიკაციაში მეორდება გამოსახულება, რომელიც შედგენილია ზედაპირის განტოლების კოეფიციენტებისაგან. კოშიმ (1829), იაკობიმ (1833) და ჰესემ (1833, 1861) ამ გამოსახულებაში დაინახეს დეტერმინანტი. ჰესემ ეს დეტერმინანტი აქცია კვლევის არსებით საშუალებად. მეორე რიგის ზედაპირების კვლევა კვეთის მეთოდით შემოიღო კოშიმ (1826-1829).

იხილე აგრეთვე

• მეორე რიგის ზედაპირები

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი