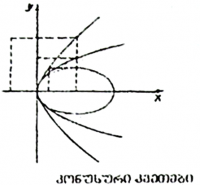
კონუსური კვეთები

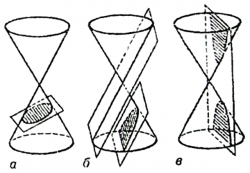
კონუსური კვეთები – ეწოდება წირებს, რომლებიც მიიღებიან წრიული კონუსის ზედაპირის იმ სიბრტყესთან გადაკვეთისას, რომელიც არ გადის კონუსის წვეროზე. კონუსურ კვეთებს სხვანაირად მეორე რიგის წირებს უწოდებენ.

თუ სიბრტყე კვეთს კონუსის ყველა მსახველს, კვეთაში მიიღება ელიფსი, (კერძო შეთხვევაში წრე).

თუ კონუსური ზედაპირი იკვეთება ერთ-ერთი მსახველის პარალელური სიბრტყით, კვეთაში მიიღება პარაბოლა.

თუ მკვეთი სიბრტყე პარალელურია კონუსური ზედაპირის ორი მსახველისა, კვეთაში მიიღება ჰიპერბოლა.

კონუსური კვეთის განტოლებას პოლარულ კოორდინატებში აქვს სახე:

სადაც r – ფოკალური (ფოკუსის) რადიუს-ვექტორია,

p – ფოკალური პარამეტრია,

e — ექსცენტრისიტეტია,

φ – პოლარული კუთხეა.

თუ e < 1, (*) განტოლება განსაზღვრავს ელიფსს (ამასთანავე 0 < φ < 2π).

e = 1, (*) განტოლება განსაზღვრავს პარაბოლს (ამასთანავე) 0< φ < 2π)

e > 1, (*) განტოლება განსაზღვრავს ჰიპერბოლას (φ₀< φ < 2π – φ₀).

კონუსური კვეთების სახის წირებს ფართოდ იყენებენ ტექნიკაში, მაგალითად, ელიფსური კბილანებში, პროჟექტორებში (პარაბოლური სარკე) და სხვ. მზის სისტემის ყველა პლანეტა მოძრაობს ელიფსზე, რომლის ერთ-ერთ ფოკუსში მოთავსებულია მზე. კომეტები მოძრაობენ როგორც ელიფსზე, ასევე პარაბოლურ და ჰიპერბოლურ ტრაექტორიაზე.

კონუსური კვეთების სახელწოდებები (ელიფსი, პარაბოლა ჰიპერბოლა) დაკავშირებულია ძველი გეომეტრების მიერ გეომეტრიულ აგებებთან.

კონუსური კვეთები უკვე ცნობილი იყო ძველ საბერძნეთში. დინოსტრატეს ძმამ და ალექსანდრე მაკედონელის მასწავლებელმა მენეხმა, დაახლოებით 340 წ. ჩვ. წ. აღ-მდე, აღმოაჩინა, რომ ელიფსი, ჰიპერბოლა და პარაბოლა წარმოადგენენ კონუსის კვეთებს. ერატოსფენმა ამ წირებს „მენეხმის ტრიადა“ უწოდა. მათი თანამედროვე სახელწოდებები შემოიღო აპოლონიოს პერგელმა, რომელმაც შედარებით უფრო სრულყოფილი კვლევა ჩაატარა, თუმცა „ელიფსი“ და „ჰიპერბოლა“ ზოგჯერ მანამდეც იხმარებოდა (მაგ., „ელიფსი“ არქიმედესაც აქვს). აპოლონმა პირველმა მიიღო ეს წირები, როგორც წრიული კონუსის ბრტყელი კვეთები და დაწვრილებით შეისწავლა მათი თვისებები; ცნობილია მისი თხზულება „კონუსური კვეთები“ (ძვ. წ. III საუკუნეში), რომელმაც დიდი გავლენა მოახდინა ასტრონომიის, მექანიკის, ოპტიკის განვითარებაზე. ამ ნაშრომს იყენებდნენ დეკარტი და ფერმა ანალიზური გეომეტრიის შექმნისას. საერთოდ კონუსური კვეთების თეორიის წარმატებები დაკავშირებულია XVII ს-ში შექმნილ ახალ გეომეტრიულ მეთოდებთან, გეგმილურ და საკოორდინატო მეთოდებთან.

კონუსური კვეთების შესწავლისას მნიშვნელოვანი შედეგები მიიღეს ბერძენმა მათემატიკოსებმა.

თანამედროვე სახელწოდებები წარმოიშვა წირებთან დაკავშირებული ბრტყელი ფიგურების ფართობების შედარებისას. თუ განვიხილავთ y²-ს, როგორც კვადრატის ფართობს, აგებულს ორდინატაზე, ხოლო 2px-ს, როგორც x გვერდისა და 2p სიმაღლის მართკუთხედის ფართობს, ვნახავთ, რომ ელიფსისათვის კვადრატის ფართობი ნაკლებია მართკუთხედის ფართობზე (ბერძნულად ελλειψιξ – „ნაკლებობა“), ჰიპერბოლის შემთხვევაში – მეტია (ιπερβολη – „ჭარბი“), ხოლო პარაბოლის შემთხვევაში ეს ფართობები ტოლია (παραβολη – „ტოლობა“).

კონუსური კვეთების დასახაზად პირველი ხელსაწყოები გამოიგონეს V და VI ს-ში პროკლემ და იზიდორე მილეთელმა. 1000 წლის შემდეგ, 1604 წ. კეპლერმა მოგვცა სამივე წირის აგების წესი თოკის საშუალებით. ერთ-ერთი მეთოდი მოიგონა კოპერნიკმა (1643). ელიფსის აგების მეთოდი გამოიგონეს ლაგირმა (1722) და ბრეიკენრიჯმა (1733).

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი