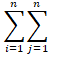უარყოფითად განსაზღვრული კვადრატული ფორმა
(ახალი გვერდი: '''უარყოფითად განსაზღვრული კვადრატული ფორმა''' – ნამდვილ [[კვა...) |
|||
| ხაზი 5: | ხაზი 5: | ||
ეწოდება უარყოფითად განსაზღვრული კვადრატული ფორმა, თუ f (x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub> )<0 ცვლადთა ნებისმიერი x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub> მნიშვნელობებისათვის, რომელთა შორისაც, თუნდაც ერთი მაინც განსხვავდება ნულისაგან. | ეწოდება უარყოფითად განსაზღვრული კვადრატული ფორმა, თუ f (x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub> )<0 ცვლადთა ნებისმიერი x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub> მნიშვნელობებისათვის, რომელთა შორისაც, თუნდაც ერთი მაინც განსხვავდება ნულისაგან. | ||
| − | + | ||
| + | '''მტკიცდება შემდეგი მნიშვნელოვანი თეორემები:''' | ||
1. თუ კვადრატული ფორმა არის უარყოფითად განსაზღვრული კვადრატული ფორმა, მაშინ უარყოფითად განსაზღვრულია მისი ეკვივალენტური ყოველი ფორმა. | 1. თუ კვადრატული ფორმა არის უარყოფითად განსაზღვრული კვადრატული ფორმა, მაშინ უარყოფითად განსაზღვრულია მისი ეკვივალენტური ყოველი ფორმა. | ||
21:57, 20 თებერვალი 2024-ის ვერსია
უარყოფითად განსაზღვრული კვადრატული ფორმა – ნამდვილ კვადრატულ ფორმას
ეწოდება უარყოფითად განსაზღვრული კვადრატული ფორმა, თუ f (x1,x2,...,xn )<0 ცვლადთა ნებისმიერი x1,x2,...,xn მნიშვნელობებისათვის, რომელთა შორისაც, თუნდაც ერთი მაინც განსხვავდება ნულისაგან.
მტკიცდება შემდეგი მნიშვნელოვანი თეორემები:
1. თუ კვადრატული ფორმა არის უარყოფითად განსაზღვრული კვადრატული ფორმა, მაშინ უარყოფითად განსაზღვრულია მისი ეკვივალენტური ყოველი ფორმა.
2 თუ n ცვლადის კვადრატული ფორმა არის უარყოფითად განსაზღვრული კვადრატული ფორმა, მაშინ n-ის ლუწი მნიშვნელობისათვის მისი მატრიცის დეტერმინანტი დადებითია, ხოლო n-ის კენტი მნიშვნელობისათვის – უარყოფითი.
3. n ცვლადის უარყოფითად განსაზღვრული კვადრატული ფორმის ნორმალური სახე შეიცავს n უარყოფით კვადრატს.
4 ნამდვილი კვადრატული ფორმა არის უარყოფითად განსაზღვრული კვადრატული ფორმა მაშინ და მხოლოდ მაშინ, როცა მისი მატრიცის ყველა მთავარი მინორი კენტი რიგისა – დადებითი, ხოლო ლუწი რიგისა – უარყოფითია.