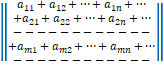ორმაგი მწკრივი
NPLG Wiki Dictionaries გვერდიდან
(სხვაობა ვერსიებს შორის)
(ახალი გვერდი: '''ორმაგი მწკრივი''' – მწკრივთა უსასრულო მიმდევრობები, რომლებ...) |
|||
| (ერთი მომხმარებლის ერთი შუალედური ვერსია არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
| − | '''ორმაგი მწკრივი''' – მწკრივთა უსასრულო მიმდევრობები, რომლებიც შეერთებულია „+“ ნიშნით; ასეთი სახით ჩაიწერება: | + | '''ორმაგი მწკრივი''' – [[მწკრივი (მათემატიკა)|მწკრივთა]] [[უსასრულობა (მათემატიკა)|უსასრულო]] [[მიმდევრობა (მათემატიკა)|მიმდევრობები]], რომლებიც შეერთებულია „+“ ნიშნით; ასეთი სახით ჩაიწერება: |
(a<sub>11</sub>+ a<sub>12</sub> + ...+ a<sub>1n</sub>+...) + ...+(a<sub>m1</sub> + a<sub>m2</sub> + ...+ a<sub>mn</sub>+...) +... | (a<sub>11</sub>+ a<sub>12</sub> + ...+ a<sub>1n</sub>+...) + ...+(a<sub>m1</sub> + a<sub>m2</sub> + ...+ a<sub>mn</sub>+...) +... | ||
| ხაზი 5: | ხაზი 5: | ||
ორმაგი მწკრივისათვის მიღებულია შემოკლებული აღნიშვნა [[ფაილი:Ormagi mw003.png]] | ორმაგი მწკრივისათვის მიღებულია შემოკლებული აღნიშვნა [[ფაილი:Ormagi mw003.png]] | ||
| − | ჩვეულებრივი მწკრივის ანალოგიურად, მნიშვნელოვანი ცნებაა ორმაგი მწკრივის კერძო ჯამი [[ფაილი:Ormagi mw005.png]] | + | ჩვეულებრივი მწკრივის ანალოგიურად, მნიშვნელოვანი ცნებაა ორმაგი მწკრივის კერძო [[ჯამი (მათემატიკა)|ჯამი]] [[ფაილი:Ormagi mw005.png]] |
| − | თუ არსებობს ზღვარი limS<sub>mn</sub>=S, როდესაც ერთმანეთისაგან დამოუკიდებლად m→∞, n→∞, მაშინ ამ ზღვარს ეწოდება ორმაგი მწკრივის ჯამი, ხოლო თვით ორმაგ მწკრივს – კრებადი. | + | თუ არსებობს [[ზღვარი (მათემატიკა)|ზღვარი]] limS<sub>mn</sub>=S, როდესაც ერთმანეთისაგან [[დამოუკიდებლობა (მათემატიკური)|დამოუკიდებლად]] m→∞, n→∞, მაშინ ამ ზღვარს ეწოდება ორმაგი მწკრივის ჯამი, ხოლო თვით ორმაგ მწკრივს – [[კრებადი მწკრივი|კრებადი]]. |
| − | '''ორმაგი მწკრივი ასეც განისაზღვრება:''' უსასრულო ||a<sub>mn</sub> || (m,n=1,2 ...) მატრიცის ელემენტებისაგან შედგენილი გამოსახულება: | + | '''ორმაგი მწკრივი ასეც განისაზღვრება:''' უსასრულო ||a<sub>mn</sub> || (m,n=1,2 ...) [[მატრიცა |მატრიცის]] ელემენტებისაგან შედგენილი გამოსახულება: |
| ხაზი 16: | ხაზი 16: | ||
| − | თუ a<sub>mn</sub> – რიცხვებია, მაშინ ორმაგ მწკრივს ეწოდება რიცხვითი; თუ a<sub>mn</sub> ერთი ან რამდენიმე ცვლადის ფუნქციაა, მაშინ ორმაგ მწკრივს ეწოდება ფუნქციონალური. | + | თუ a<sub>mn</sub> – [[რიცხვი (მათემატიკა)|რიცხვებია]], მაშინ ორმაგ მწკრივს ეწოდება რიცხვითი; თუ a<sub>mn</sub> ერთი ან რამდენიმე [[ცვლადი|ცვლადის]] [[ფუნქცია (მათემატიკური)|ფუნქციაა]], მაშინ ორმაგ მწკრივს ეწოდება ფუნქციონალური. |
==წყარო== | ==წყარო== | ||
მიმდინარე ცვლილება 12:56, 2 აპრილი 2024 მდგომარეობით
ორმაგი მწკრივი – მწკრივთა უსასრულო მიმდევრობები, რომლებიც შეერთებულია „+“ ნიშნით; ასეთი სახით ჩაიწერება:
(a11+ a12 + ...+ a1n+...) + ...+(am1 + am2 + ...+ amn+...) +...
ორმაგი მწკრივისათვის მიღებულია შემოკლებული აღნიშვნა ![]()
ჩვეულებრივი მწკრივის ანალოგიურად, მნიშვნელოვანი ცნებაა ორმაგი მწკრივის კერძო ჯამი ![]()
თუ არსებობს ზღვარი limSmn=S, როდესაც ერთმანეთისაგან დამოუკიდებლად m→∞, n→∞, მაშინ ამ ზღვარს ეწოდება ორმაგი მწკრივის ჯამი, ხოლო თვით ორმაგ მწკრივს – კრებადი.
ორმაგი მწკრივი ასეც განისაზღვრება: უსასრულო ||amn || (m,n=1,2 ...) მატრიცის ელემენტებისაგან შედგენილი გამოსახულება:
თუ amn – რიცხვებია, მაშინ ორმაგ მწკრივს ეწოდება რიცხვითი; თუ amn ერთი ან რამდენიმე ცვლადის ფუნქციაა, მაშინ ორმაგ მწკრივს ეწოდება ფუნქციონალური.