კონუსი
| (ერთი მომხმარებლის 3 შუალედური ვერსიები არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
'''კონუსი, კონუსური ზედაპირი''' – კონუსი (ანუ კონუსური ზედაპირი) – სივრცის იმ წრფეების (მსახველების) გეომეტრიული ადგილია, რომლებიც აერთებენ რაიმე წირის (მიმმართველის) ყველა წერტილს სივრცის მოცემულ წერტილთან (წვეროსთან). ეს წირი (მიმმართველი) და წერტილი (წვერო) ერთ სიბრტყეში არ მდებარეობენ. | '''კონუსი, კონუსური ზედაპირი''' – კონუსი (ანუ კონუსური ზედაპირი) – სივრცის იმ წრფეების (მსახველების) გეომეტრიული ადგილია, რომლებიც აერთებენ რაიმე წირის (მიმმართველის) ყველა წერტილს სივრცის მოცემულ წერტილთან (წვეროსთან). ეს წირი (მიმმართველი) და წერტილი (წვერო) ერთ სიბრტყეში არ მდებარეობენ. | ||
| + | [[ფაილი:Konusi.PNG|მარჯვნივ|]] | ||
კონუსურ ზედაპირს აქვს ორი სიღრუვე, რომლებიც წვეროს მიმართ სიმეტრიულად არიან განლაგებულნი. | კონუსურ ზედაპირს აქვს ორი სიღრუვე, რომლებიც წვეროს მიმართ სიმეტრიულად არიან განლაგებულნი. | ||
| ხაზი 25: | ხაზი 26: | ||
ხოლო გვერდითი ზედაპირის ფართობი S=π(R + r) ℓ. | ხოლო გვერდითი ზედაპირის ფართობი S=π(R + r) ℓ. | ||
| − | ბერძნული κωνοξ – „ნაძვის გირჩი“, „მუზარადის წვეტიანი ბოლო“. ტერმინს თანამედროვე აზრით იყენებდნენ ევკლიდე, არისტარხი, არქიმედე. კონუსის მოცულობა პირველად გამოთვალა ჰერონ ალექსანდრიელმა. გვერდითი ზედაპირის (კონუსის და ცილინდრის) ფართობი მოძებნა არქიმედემ. არქიმედეს გადმოცემით, დემოკრიტემ აღმოაჩინა, რომ კონუსის (პირამიდის) მოცულობა შეადგენს იმავე ფუძისა და სიმაღლის ცილინდრის (პრიზმის) მოცულობის მესამედს. ეს პირველად დაამტკიცა ევდოქსმა. | + | ბერძნული κωνοξ – „ნაძვის გირჩი“, „მუზარადის წვეტიანი ბოლო“. ტერმინს თანამედროვე აზრით იყენებდნენ ევკლიდე, არისტარხი, არქიმედე. კონუსის მოცულობა პირველად გამოთვალა [[ჰერონ ალექსანდრიელი|ჰერონ ალექსანდრიელმა]]. გვერდითი ზედაპირის (კონუსის და ცილინდრის) ფართობი მოძებნა არქიმედემ. არქიმედეს გადმოცემით, დემოკრიტემ აღმოაჩინა, რომ კონუსის (პირამიდის) მოცულობა შეადგენს იმავე ფუძისა და სიმაღლის ცილინდრის (პრიზმის) მოცულობის მესამედს. ეს პირველად დაამტკიცა ევდოქსმა. |
მიმდინარე ცვლილება 12:48, 19 დეკემბერი 2024 მდგომარეობით
კონუსი, კონუსური ზედაპირი – კონუსი (ანუ კონუსური ზედაპირი) – სივრცის იმ წრფეების (მსახველების) გეომეტრიული ადგილია, რომლებიც აერთებენ რაიმე წირის (მიმმართველის) ყველა წერტილს სივრცის მოცემულ წერტილთან (წვეროსთან). ეს წირი (მიმმართველი) და წერტილი (წვერო) ერთ სიბრტყეში არ მდებარეობენ.
კონუსურ ზედაპირს აქვს ორი სიღრუვე, რომლებიც წვეროს მიმართ სიმეტრიულად არიან განლაგებულნი.
მეორე რიგის კონუსური ზედაპირი არის მეორე რიგის ზედაპირების ერთ-ერთი სახე.
მეორე რიგის ნამდვილი კონუსური ზედაპირის კანონიკური განტოლება ასეთი სახისაა:
თუ a = b, მაშინ კონუსურ ზედაპირს ეწოდება წრიული, ანუ ბრუნვის კონუსური ზედაპირი.
მეორე რიგის წარმოსახვითი კონუსური ზედაპირის კანონიკური განტოლება ასეთი სახისაა:
ასეთ კონუსურ ზედაპირს აქვს ერთად ერთი ნამდვილი წერტილი 0(0,0,0).
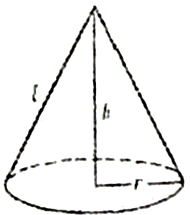
მიმმართველის მიხედვით კონუსი შეიძლება იყოს წრიული, ელიფსური და სხვ. კონუსებს შორის უმარტივესია წრიული კონუსური ზედაპირი, რომლის მიმმართველია წრეწირი, ხოლო წვერო ორთოგონალურად გეგმილდება მის ცენტრში. წრიული კონუსი წარმოადგენს გეომეტრიულ სხეულს, რომელიც შემოსაზღვრულია წრიული კონუსის ზედაპირით და მიმმართველი წრეწირის მომცველი სიბრტყით. ასეთი კონუსის მოცულობა 
(r – კონუსის ფუძის რადიუსია, h – კონუსის სიმაღლე). გვერდითი ზედაპირის ფართობი S=πrℓ (ℓ – მსახველის სიგრძეა).
თუ კონუსს გადავკვეთთ სიბრტყით, რომელიც ფუძის სიბრტყის პარალელურია, მაშინ მიიღება წაკვეთილი კონუსი, რომლის მოცულობაა
ხოლო გვერდითი ზედაპირის ფართობი S=π(R + r) ℓ.
ბერძნული κωνοξ – „ნაძვის გირჩი“, „მუზარადის წვეტიანი ბოლო“. ტერმინს თანამედროვე აზრით იყენებდნენ ევკლიდე, არისტარხი, არქიმედე. კონუსის მოცულობა პირველად გამოთვალა ჰერონ ალექსანდრიელმა. გვერდითი ზედაპირის (კონუსის და ცილინდრის) ფართობი მოძებნა არქიმედემ. არქიმედეს გადმოცემით, დემოკრიტემ აღმოაჩინა, რომ კონუსის (პირამიდის) მოცულობა შეადგენს იმავე ფუძისა და სიმაღლის ცილინდრის (პრიზმის) მოცულობის მესამედს. ეს პირველად დაამტკიცა ევდოქსმა.
