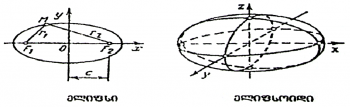
ელიფსი
(ახალი გვერდი: 350px '''ელიფსი''' – ბრტყელი წირი, რომელიც სი...) |
|||
| (ერთი მომხმარებლის ერთი შუალედური ვერსია არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
[[ფაილი:Elifsi.PNG|მარჯვნივ|350px]] | [[ფაილი:Elifsi.PNG|მარჯვნივ|350px]] | ||
| − | '''ელიფსი''' – [[ბრტყელი წირი]], რომელიც სიბრტყის იმ [[ | + | '''ელიფსი''' – [[ბრტყელი წირი]], რომელიც [[სიბრტყე (გეომეტრია)|სიბრტყის]] იმ [[წერტილი (გეომეტრია)|წერტილთა]] [[გეომეტრიული ადგილი]]ა, რომელთათვისაც ამ სიბრტყის ორ მოცემულ F<sub>1</sub> და F<sub>2</sub> წერტილებამდე (ელიფსის [[ფოკუსი|ფოკუსებამდე]]) [[მანძილი (გეომეტრია)|მანძილების]] [[ჯამი (მათემატიკა)|ჯამი]] მოცემული [[მუდმივი სიდიდე]]ა და უდრის 2a-ს (2a>F<sub>1</sub> F<sub>2</sub>). მოცემულ 2a [[რიცხვი (მათემატიკა)|რიცხვს]] ([[მონაკვეთი (გეომეტრია)|მონაკვეთს]]) ელიფსის დიდ [[ღერძი|ღერძს]] უწოდებენ. ფოკუსებს შორის მანძილს ფოკალური მანძილი ეწოდება და უდრის 2c-ს. [[დეკარტის კოორდინატთა სისტემა|დეკარტეს მართკუთხა კოორდინატთა სისტემაში]] ელიფსის უმარტივეს ([[კანონიკური განტოლება|კანონიკურ]]) [[განტოლება]]ს აქვს ასეთი სახე: [[ფაილი:Image219.png]] სადაც b<sup>2</sup>=a<sup>2</sup>-c<sup>2</sup>. |
| − | 2b | + | 2b [[სიდიდე (მათემატიკა)|სიდიდე]]ს (მონაკვეთს) ელიფსის მცირე ღერძი ეწოდება. |
| − | ელიფსის პარამეტრულ განტოლებას აქვს სახე: | + | ელიფსის [[პარამეტრი (მათემატიკა)|პარამეტრულ]] განტოლებას აქვს სახე: |
:::::x=a cost, y=b sint. | :::::x=a cost, y=b sint. | ||
| − | e = c/a სიდიდეს ელიფსის ექსცენტრისიტეტი ეწოდება. ელიფსისათვის c<1. | + | e = c/a სიდიდეს ელიფსის [[ექსცენტრისიტეტი]] ეწოდება. ელიფსისათვის c<1. |
| − | F<sub>1</sub> F<sub>2</sub> მონაკვეთის შუა [[წერტილი (გეომეტრია)|წერტილს]] ელიფსის ცენტრს უწოდებენ. ელიფსის ცენტრზე გამავალ ნებისმიერ | + | F<sub>1</sub> F<sub>2</sub> მონაკვეთის შუა [[წერტილი (გეომეტრია)|წერტილს]] ელიფსის [[ცენტრი (გეომეტრია)|ცენტრს]] უწოდებენ. ელიფსის ცენტრზე გამავალ ნებისმიერ [[წრფე]]ს ელიფსის [[დიამეტრი]] ეწოდება. |
| − | + | წრფეს, რომლის განტოლებაა x=±a/b, ელიფსის [[დირექტრისა]] ეწოდება. | |
| − | ელიფსი მიიღება, როგორც წრიული კონუსის გადაკვეთის წირი იმ სიბრტყესთან, რომელიც კვეთს ამ კონუსის ერთ-ერთი კალთის ყველა მსახველს. | + | ელიფსი მიიღება, როგორც წრიული [[კონუსი|კონუსის]] [[გადაკვეთა|გადაკვეთის]] [[წირი]] იმ სიბრტყესთან, რომელიც კვეთს ამ კონუსის ერთ-ერთი კალთის ყველა [[მსახველი (წრფივი)|მსახველს]]. |
სახელწოდება „ელიფსი“ წარმოიშვა ბერძნული სიტყვიდან elleipsis – „ნაკლი“, „დანაკლისი“, რაც გამოხატავს იმ აზრს, რომ ელიფსის ექსცენტრისიტეტს აკლია 1-მდე (c<1) | სახელწოდება „ელიფსი“ წარმოიშვა ბერძნული სიტყვიდან elleipsis – „ნაკლი“, „დანაკლისი“, რაც გამოხატავს იმ აზრს, რომ ელიფსის ექსცენტრისიტეტს აკლია 1-მდე (c<1) | ||
| + | |||
| + | ==წყარო== | ||
| + | [[მათემატიკის ენციკლოპედიური ლექსიკონი]] | ||
| + | |||
| + | [[კატეგორია:მათემატიკა]] | ||
| + | [[კატეგორია:გეომეტრია]] | ||
მიმდინარე ცვლილება 20:50, 13 აპრილი 2024 მდგომარეობით
ელიფსი – ბრტყელი წირი, რომელიც სიბრტყის იმ წერტილთა გეომეტრიული ადგილია, რომელთათვისაც ამ სიბრტყის ორ მოცემულ F1 და F2 წერტილებამდე (ელიფსის ფოკუსებამდე) მანძილების ჯამი მოცემული მუდმივი სიდიდეა და უდრის 2a-ს (2a>F1 F2). მოცემულ 2a რიცხვს (მონაკვეთს) ელიფსის დიდ ღერძს უწოდებენ. ფოკუსებს შორის მანძილს ფოკალური მანძილი ეწოდება და უდრის 2c-ს. დეკარტეს მართკუთხა კოორდინატთა სისტემაში ელიფსის უმარტივეს (კანონიკურ) განტოლებას აქვს ასეთი სახე: ![]() სადაც b2=a2-c2.
სადაც b2=a2-c2.
2b სიდიდეს (მონაკვეთს) ელიფსის მცირე ღერძი ეწოდება.
ელიფსის პარამეტრულ განტოლებას აქვს სახე:
- x=a cost, y=b sint.
e = c/a სიდიდეს ელიფსის ექსცენტრისიტეტი ეწოდება. ელიფსისათვის c<1.
F1 F2 მონაკვეთის შუა წერტილს ელიფსის ცენტრს უწოდებენ. ელიფსის ცენტრზე გამავალ ნებისმიერ წრფეს ელიფსის დიამეტრი ეწოდება.
წრფეს, რომლის განტოლებაა x=±a/b, ელიფსის დირექტრისა ეწოდება.
ელიფსი მიიღება, როგორც წრიული კონუსის გადაკვეთის წირი იმ სიბრტყესთან, რომელიც კვეთს ამ კონუსის ერთ-ერთი კალთის ყველა მსახველს.
სახელწოდება „ელიფსი“ წარმოიშვა ბერძნული სიტყვიდან elleipsis – „ნაკლი“, „დანაკლისი“, რაც გამოხატავს იმ აზრს, რომ ელიფსის ექსცენტრისიტეტს აკლია 1-მდე (c<1)