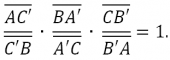ჩევის თეორემა
NPLG Wiki Dictionaries გვერდიდან
(სხვაობა ვერსიებს შორის)
| ხაზი 3: | ხაზი 3: | ||
:::::[[ფაილი:Chevis Teorema1.PNG|170px|]] | :::::[[ფაილი:Chevis Teorema1.PNG|170px|]] | ||
| − | ამასთანავე, [[ვექტორი|ვექტორთა]] შეფარდება განიხილება, როგორც დადებითი, თუ მათ აქვთ ერთი და იგივე მიმართულება (მაგალითად, [[ფაილი:Chevis Teorema2.PNG|23px|]] -ს და [[ფაილი:Chevis Teorema3.PNG|23px|]] -ს) და უარყოფითი – საპირისპირო შემთხვევაში. | + | ამასთანავე, [[ვექტორი|ვექტორთა]] [[შეფარდება (მათემატიკა)|შეფარდება]] განიხილება, როგორც დადებითი, თუ მათ აქვთ ერთი და იგივე [[მიმართულება (მათემატიკური)|მიმართულება]] (მაგალითად, [[ფაილი:Chevis Teorema2.PNG|23px|]] -ს და [[ფაილი:Chevis Teorema3.PNG|23px|]] -ს) და უარყოფითი – საპირისპირო შემთხვევაში. |
15:39, 18 სექტემბერი 2023-ის ვერსია
ჩევის თეორემა – თუ წრფეები, რომლებიც ABC სამკუთხედის წვეროებს აერთებენ სამკუთხედის შიგნით მდებარე 0 წერტილთან, კვეთენ მოპირდაპირე გვერდებს ან მათ გაგრძელებებს შესაბამისად A', B', C' წერტილებში, მაშინ მართებულია ტოლობა:
ამასთანავე, ვექტორთა შეფარდება განიხილება, როგორც დადებითი, თუ მათ აქვთ ერთი და იგივე მიმართულება (მაგალითად, -ს და
-ს) და უარყოფითი – საპირისპირო შემთხვევაში.