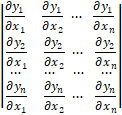იაკობიანი
NPLG Wiki Dictionaries გვერდიდან
(სხვაობა ვერსიებს შორის)
| ხაზი 9: | ხაზი 9: | ||
სახელი ეწოდება გერმანელი მათემატიკოსის კ. იაკობის პატივსაცემად. | სახელი ეწოდება გერმანელი მათემატიკოსის კ. იაკობის პატივსაცემად. | ||
| − | „იაკობიანით“ უკვე სარგებლობდა [[ეილერი ლეონარდ|ეილერი]] ახალ ცვლადებზე გადასვლისას (1759 – 1770). ზოგადი ფუნქციონალური დეტერმინანტი თანამედროვე სახით პირველად შემოიღო იაკობიმ (1841). აღნიშვნა ∂(f<sub>1</sub>,f<sub>2</sub>,...,f<sub>n</sub>) / ∂(x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub>) ეკუთვნის დონკინს (1854), ხოლო J(f<sub>1</sub>,f<sub>2</sub>,...,f<sub>n</sub>) – უელდის (1896). ტერმინი „იაკობიანი“ შემოიღეს კელიმ და სილვესტრმა (1956), რათა პატივი მიეგოთ იაკობის შრომებისათვის [[ალგებრა]]ში და გამორიცხვის [[თეორია]]ში. | + | „იაკობიანით“ უკვე სარგებლობდა [[ეილერი ლეონარდ|ეილერი]] ახალ ცვლადებზე გადასვლისას (1759 – 1770). ზოგადი [[ფუნქციონალური დეტერმინანტი]] თანამედროვე სახით პირველად შემოიღო იაკობიმ (1841). აღნიშვნა ∂(f<sub>1</sub>,f<sub>2</sub>,...,f<sub>n</sub>) / ∂(x<sub>1</sub>,x<sub>2</sub>,...,x<sub>n</sub>) ეკუთვნის დონკინს (1854), ხოლო J(f<sub>1</sub>,f<sub>2</sub>,...,f<sub>n</sub>) – უელდის (1896). ტერმინი „იაკობიანი“ შემოიღეს კელიმ და სილვესტრმა (1956), რათა პატივი მიეგოთ იაკობის შრომებისათვის [[ალგებრა]]ში და გამორიცხვის [[თეორია]]ში. |
მიმდინარე ცვლილება 23:24, 3 ივლისი 2024 მდგომარეობით
იაკობიანი – იაკობის ფუნქციონალური დეტერმინანტი |aik|, სადაც aik=∂yi/∂xk, რომელიც შედგება მოცემული n ფუნქციის y1,y2,...,yn კერძო წარმოებულებისაგან ერთი და იგივე x1,x2,...,xn ცვლადებით:
მოკლედ ასე აღინიშნება:
სახელი ეწოდება გერმანელი მათემატიკოსის კ. იაკობის პატივსაცემად.
„იაკობიანით“ უკვე სარგებლობდა ეილერი ახალ ცვლადებზე გადასვლისას (1759 – 1770). ზოგადი ფუნქციონალური დეტერმინანტი თანამედროვე სახით პირველად შემოიღო იაკობიმ (1841). აღნიშვნა ∂(f1,f2,...,fn) / ∂(x1,x2,...,xn) ეკუთვნის დონკინს (1854), ხოლო J(f1,f2,...,fn) – უელდის (1896). ტერმინი „იაკობიანი“ შემოიღეს კელიმ და სილვესტრმა (1956), რათა პატივი მიეგოთ იაკობის შრომებისათვის ალგებრაში და გამორიცხვის თეორიაში.