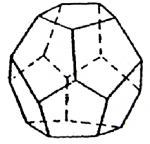
დოდეკაედრი
NPLG Wiki Dictionaries გვერდიდან
(სხვაობა ვერსიებს შორის)
(ახალი გვერდი: '''დოდეკაედრი''' – თორმეტწახნაგა. ტერმინი წარმომდგარია ბერძნუ...) |
|||
| ხაზი 1: | ხაზი 1: | ||
| − | '''დოდეკაედრი''' | + | '''დოდეკაედრი''' (''ბერძ''. δωδεκα – „თორმეტი“ და εδρα – „ფუძე“) – თორმეტწახნაგა. |
[[ფაილი:Dodekaedri.png|მარჯვნივ|150პქ]] | [[ფაილი:Dodekaedri.png|მარჯვნივ|150პქ]] | ||
| − | + | [[მათემატიკა]]ში ჩვეულებრივ იხილავენ წესიერ დოდეკაედრს – წესიერ თორმეტწახნაგას. წესიერ დოდეკაედრს აქვს 12 წესიერი ხუთკუთხა [[წახნაგი]], 30 [[წიბო]], 20 [[წვერო]]. თითოეულ წვეროში თავს იყრის 3 წიბო. ყოველ წესიერ დოდეკაედრში შეიძლება ჩაიწეროს [[სფერო]] და შეიძლება მასზე შემოიწეროს სფერო. თუ დოდეკაედრის წიბოს [[სიგრძე (მათემატიკა)|სიგრძე]]ა a, მაშინ მისი [[მოცულობა (გეომეტრია)|მოცულობა]] | |
::::V=1/4 · a<sup>3</sup> (15+7 √<span style="box-sizing: border-box;tures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; ohans: 2; text-align: center; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; text-decoration: overline">3</span>) ≈ 7,6631 a<sup>3</sup>. | ::::V=1/4 · a<sup>3</sup> (15+7 √<span style="box-sizing: border-box;tures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; ohans: 2; text-align: center; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; text-decoration: overline">3</span>) ≈ 7,6631 a<sup>3</sup>. | ||
| − | დოდეკაედრი უკვე ცნობილი იყო პითაგორელებისათვის. იგი პირველად ააგო თეეტეტმა (IV ს. ჩვ. წ. აღ-მდე). | + | დოდეკაედრი უკვე ცნობილი იყო პითაგორელებისათვის. იგი პირველად ააგო [[თეეტეტი ათენელი|თეეტეტმა]] (IV ს. ჩვ. წ. აღ-მდე). |
მიმდინარე ცვლილება 13:57, 5 ივლისი 2024 მდგომარეობით
დოდეკაედრი (ბერძ. δωδεκα – „თორმეტი“ და εδρα – „ფუძე“) – თორმეტწახნაგა.
მათემატიკაში ჩვეულებრივ იხილავენ წესიერ დოდეკაედრს – წესიერ თორმეტწახნაგას. წესიერ დოდეკაედრს აქვს 12 წესიერი ხუთკუთხა წახნაგი, 30 წიბო, 20 წვერო. თითოეულ წვეროში თავს იყრის 3 წიბო. ყოველ წესიერ დოდეკაედრში შეიძლება ჩაიწეროს სფერო და შეიძლება მასზე შემოიწეროს სფერო. თუ დოდეკაედრის წიბოს სიგრძეა a, მაშინ მისი მოცულობა
- V=1/4 · a3 (15+7 √3) ≈ 7,6631 a3.
დოდეკაედრი უკვე ცნობილი იყო პითაგორელებისათვის. იგი პირველად ააგო თეეტეტმა (IV ს. ჩვ. წ. აღ-მდე).