მეორე რიგის ზედაპირები

მიმდინარე ცვლილება 15:59, 16 აპრილი 2024 მდგომარეობით

მეორე რიგის ზედაპირები – სამგანზომილებიანი ევკლიდეს სივრცის წერტილთა სიმრავლე, რომელთა x, y, z კოორდინატები აკმაყოფილებენ მე-2 ხარისხის ალგებრულ განტოლებას:

a₁₁ x² + a₂₂ y² + a₃₃z² + 2a₁₂xy + 2a₁₃xz + 2a₂₃уz+2a₁₄x + 2a₂₄y + 2a₃₄z + a₄₄ = 0, (*)

სადაც ზოგიერთი a_ij კოეფიციენტი ნულისაგან განსხვავდება (i, j = 1, 2, 3).

კოეფიციენტებზე დამოკიდებულების მიხედვით (*) განტოლება კოორდინატთა მართკუთხა სისტემაში დაიყვანება შემდეგ ერთ-ერთ კანონიკურ სახეზე.

არადაშლადი ზედაპირები:

გ ა დ ა უ გ ვ ა რ ე ბ ე ლ ი:

ელიფსური –

1. 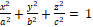– ელიფსოიდი,

2. 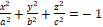– წარმოსახვითი ელიფსოიდი,

ჰიპერბოლური –

3. 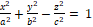– ცალკალთა ჰიპერბოლოიდი,

4. 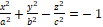– ორკალთა ჰიპერბოლოიდი,

პარაბოლური (p>0, q>0) -

5. 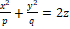– ელიფსური პარაბოლოიდი,

6. 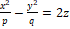– ჰიპერბოლური პარაბოლოიდი.

გ ა დ ა გ ვ ა რ ე ბ უ ლ ი:

ცილინდრული –

7. – ელიფსური ცილინდრი,

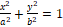8. – წარმოსახვითი ელიფსური ცილინდრი,

9. 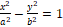– ჰიპერბოლური ცილინდრი,

10. y² = 2px – პარაბოლური ცილინდრი.

კონუსური —

11. – კონუსი,

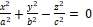12. – წარმოსახვითი კონუსი.

დაშლადი გადაგვარებული ზედაპირები:

13. – გადამკვეთ სიბრტყეთა წყვილი,

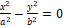14. – წარმოსახვით გადამკვეთ სიბრტყეთა წყვილი,

15. x² = a² – პარალელურ სიბრტყეთა წყვილი,

16. x² = -a² – წარმოსახვით პარალელურ სიბრტყეთა წყვილი,

17. x² = 0 – თანამთხვევად სიბრტყეთა წყვილი.

(*) განტოლებამ შეიძლება არ განსაზღვროს ნამდვილი გეომეტრიული სახე, მაგრამ ზოგადობის შესანარჩუნებლად ასეთ შემთხვევაში ამბობენ, რომ ის განსაზღვრავს მეორე რიგის წარმოსახვით ზედაპირს. მაგალითად, ზემოთ, მე-2, მე-8 და მე-16 განტოლებები არ წარმოადგენენ არავითარ გეომეტრიულ სახეს, მაგრამ ამბობენ, რომ ისინი შესაბამისად წარმოადგენენ წარმოსახვით ელიფსოიდს (2), წარმოსახვით ელიფსურ ცილინდრს (8) და წარმოსახვით პარალელურ სიბრტყეთა წყვილს (16). მე-12 განტოლება წარმოადგენს მხოლოდ ერთ წერტილს (0,0,0), მაგრამ (მე-11 განტოლებასთან მსგავსების გამო) ამბობენ, რომ იგი წარმოადგენს მეორე რიგის წარმოსახვით კონუსს, ნამდვილი წვეროთი. მე-14 განტოლება წარმოადგენს არა ზედაპირს, არამედ წრფეს (x = 0, y = 0), მაგრამ, ამბობენ, რომ იგი წარმოადგენს წარმოსახვით სიბრტყეთა წყვილს (რომლებიც ნამდვილ წრფეზე იკვეთებიან). თუ ვისარგებლებთ ამ პირობითი ტერმინებით, შეიძლება ითქვას, რომ მეორე რიგის ყოველი ზედაპირი წარმოადგენს ერთ-ერთს ზემოთ ჩამოთვლილებიდან. („ზედაპირები მეორე რიგის“).

მეორე რიგის ზედაპირები მე-2 ხარისხის განტოლებების სახით პირველად ლ. ეილერმა წარმოადგინა (1748). თანამედროვე სახელწოდება გადაუგვარებელი მეორე რიგის ზედაპირებისათვის მოგვცა გ. მონჟიმ (1801).

[რედაქტირება] წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი