ეილერის იგივეობები
NPLG Wiki Dictionaries გვერდიდან
ეილერის იგივეობები
1) ეილერის იგივეობა მარტივი რიცხვების შესახებ:
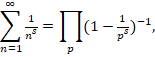 სადაც s >1 – ნებისმიერი ნამდვილი რიცხვია; ნამრავლი აიღება ყველა მარტივი p რიცხვისათვის.
სადაც s >1 – ნებისმიერი ნამდვილი რიცხვია; ნამრავლი აიღება ყველა მარტივი p რიცხვისათვის.
ეს იგივეობა მართებულია ყველა კომპლექსური რიცხვისთვისაც s=a+bi, როცა a>1.
2) ეილერის იგივეობა ოთხი კვადრატის შესახებ:
- (a2+b2+c2+d2) ∙ (p2+q2+r2+s2) = (ap+bq+cr+ds)2 + (aq-bp±cs∓dr)2 + (ar∓bs-cp±dq)2 + (as±br∓cq-dp)2