ახარისხება
NPLG Wiki Dictionaries გვერდიდან
(სხვაობა ვერსიებს შორის)
(ახალი გვერდი: '''ახარისხება''' – თავის თავზე გამრავლება, ხარისხში აყვანა. ==წ...) |
|||
| (ერთი მომხმარებლის 3 შუალედური ვერსიები არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
| − | '''ახარისხება''' – თავის თავზე გამრავლება, ხარისხში აყვანა. | + | '''ახარისხება''' – თავის თავზე [[გამრავლება |გამრავლება]], [[ხარისხი (მათემატიკა)|ხარისხში]] აყვანა. |
| + | |||
| + | |||
| + | '''სხვადასხვა ფორმულები:''' | ||
| + | |||
| + | :(a±b)<sup>2</sup> = a<sup>2</sup> ± 2ab + b<sup>2</sup>, | ||
| + | :(a±b)<sup>3</sup> = a<sup>3</sup> ± 3a<sup>2</sup> b + 3ab<sup>2</sup> ± b<sup>3</sup>, | ||
| + | :(a±b)<sup>4</sup> = a<sup>4</sup> ± 4a<sup>3</sup>b + 6a<sup>2</sup>b<sup>2</sup> ± 4ab<sup>3</sup> + b<sup>4</sup>, | ||
| + | :- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - | ||
| + | :(a + b)<sup>n</sup> =[[ფაილი:Sxvadasxva001.png]] [[ფაილი:Juf003.png]] a<sup>n-m</sup>b<sup>m</sup> (n=1,2,…), სადაც [[ფაილი:Sxvadasxva003.png]] | ||
| + | |||
| + | |||
| + | :(a + b + c)<sup>2</sup> = a<sup>2</sup> + b<sup>2</sup> + c<sup>2</sup> + 2ab + 2ac + 2bc; | ||
| + | |||
| + | |||
| + | :a<sup>2</sup> - b<sup>2</sup> = (a + b)(a - b); | ||
| + | :a<sup>2</sup> + b<sup>2</sup> = (a + ib)(a - ib); | ||
| + | :a<sup>3</sup> ± b<sup>3</sup> = (a ± b)(a<sup>2</sup> ∓ ab + b<sup>2</sup>). | ||
| + | :(a<sup>n</sup> ± b<sup>n</sup>) = (a ± b)[a<sup>n-1</sup> ∓ a<sup>n-2</sup> b ± a<sup>n-3</sup> b<sup>2</sup> ∓ ⋯ + (∓1)<sup>n-1</sup> b<sup>n-1</sup>]. | ||
| + | |||
| + | |||
| + | :a<sup>4</sup> + a<sup>2</sup> b<sup>2</sup> + b<sup>4</sup> = (a<sup>2</sup> + ab + b<sup>2</sup>)(a<sup>2</sup> - ab + b<sup>2</sup>). | ||
| ხაზი 6: | ხაზი 27: | ||
[[კატეგორია:მათემატიკა]] | [[კატეგორია:მათემატიკა]] | ||
| + | [[კატეგორია:ფორმულები]] | ||
მიმდინარე ცვლილება 16:24, 20 დეკემბერი 2023 მდგომარეობით
ახარისხება – თავის თავზე გამრავლება, ხარისხში აყვანა.
სხვადასხვა ფორმულები:
- (a±b)2 = a2 ± 2ab + b2,
- (a±b)3 = a3 ± 3a2 b + 3ab2 ± b3,
- (a±b)4 = a4 ± 4a3b + 6a2b2 ± 4ab3 + b4,
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
- (a + b)n =
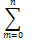
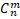an-mbm (n=1,2,…), სადაც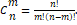 
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc;
- a2 - b2 = (a + b)(a - b);
- a2 + b2 = (a + ib)(a - ib);
- a3 ± b3 = (a ± b)(a2 ∓ ab + b2).
- (an ± bn) = (a ± b)[an-1 ∓ an-2 b ± an-3 b2 ∓ ⋯ + (∓1)n-1 bn-1].
- a4 + a2 b2 + b4 = (a2 + ab + b2)(a2 - ab + b2).
