ელიფსური კოორდინატები სიბრტყეზე

NPLG Wiki Dictionaries გვერდიდან

21:39, 29 ივნისი 2024-ის ვერსია, შეტანილი Echelidze (განხილვა | წვლილი)-ის მიერ

(განსხ.) ←წინა ვერსია | მიმდინარე ვერსია (განსხ.) | შემდეგი ვერსია→ (განსხ.)

გადასვლა: ნავიგაცია, ძიება

ელიფსური კოორდინატები სიბრტყეზე – σ და τ რიცხვები, რომლებიც დეკარტეს მართკუთხა კოორდინატებთან დაკავშირებულია ფორმულებით:

Elifsuri koordinatebi sibrtyeze.PNG

x² = (σ+ a²) (τ+ a²) / (a²- b²),

y² = (σ + b²) (τ + b²) / (b² - a²),

სადაც – a² < τ < -b² < σ < ∞.

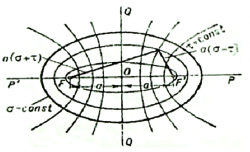
ელიფსური კოორდინატები დაკავშირებულია თანაფოკუსიანი ელიფსების და ჰიპერბოლების ოჯახთან. საკოორდინატო წირებია თანაფოკუსიანი ელიფსები (σ =const) და თანაფოკუსიანი ჰიპერბოლები (τ = const) ფოკუსებით (- ,0) და (,0) წერტილებში. σ და τ რიცხვების ყოველ წყვილს 0xy სიბრტყის ყოველ კვადრანტზე შეესაბამება 4 წერტილი, რომლებიც ერთმანეთის სიმეტრიულია 0x და 0y ღერძების მიმართ.

ელიფსური კოორდინატების სისტემა ორთოგონალურია.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი

მოძიებულია „https://www.nplg.gov.ge/wikidict/index.php?title=%E1%83%94%E1%83%9A%E1%83%98%E1%83%A4%E1%83%A1%E1%83%A3%E1%83%A0%E1%83%98_%E1%83%99%E1%83%9D%E1%83%9D%E1%83%A0%E1%83%93%E1%83%98%E1%83%9C%E1%83%90%E1%83%A2%E1%83%94%E1%83%91%E1%83%98_%E1%83%A1%E1%83%98%E1%83%91%E1%83%A0%E1%83%A2%E1%83%A7%E1%83%94%E1%83%96%E1%83%94&oldid=230548“-დან

კატეგორია:

მათემატიკა

პირადი ხელსაწყოები

ხელსაწყოები