ლოპიტალის წესი

ლოპიტალის წესი – 0/0 ან ∞/∞ სახის განუზღვრელობის გახსნის წესი.

სახის ზღვრის გამოთვლის წესი, როდესაც

ეს წესი შემდეგში მდგომარეობს: თუ f(x) და g(x) ფუნქციები წარმოებადია x=x₀ წერტილის რაიმე არეში (შესაძლოა თვით x=x₀-ის გამოკლებით) და არსებობს ზღვარი.

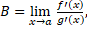მაშინ გვაქვს ტოლობა:

ლოპიტალის წესი გამოიყენება სხვადასხვა სახის განუზღვრელობის გასახსნელად: o/ o, ∞ /∞, ∞ - ∞, 0 - ∞, 0⁰, 1^∞, ∞⁰. იმ შემთხვევაში, თუ, მაგალითად,

შეიძლება ლოპიტალის წესის განმეორებით გამოყენება:

ამ წესის გამოყენება შეიძლება რამდენიმეჯერ.

ლოპიტალის წესი წარმოადგენს ზღვრების გამოთვლის საკმაოდ ძლიერ იარაღს. ეს წესი ფრანგმა მათემატიკოსმა გ. ლოპიტალმა პირველად გამოაქვეყნა დიფერენციალური აღრიცხვის პირველ ნაბეჭდ სახელმძღვანელოში (1696); მას საფუძვლად დაედო შვეიცარიელი მეცნიერის ი. ბერნულის ლექციები, რომლისთვისაც ცნობილი იყო ლოპიტალის წესი.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი