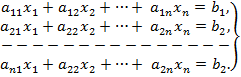წრფივი განტოლება

წრფივი განტოლება – განტოლება, რომელიც უცნობს შეიცავს პირველ ხარისხში; მაგალითად, a₁x₁+a₂ x₂+...+a_n x_n=b სახის ალგებრული განტოლება, სადაც x₁,x₂,...,x_n – უცნობი სიდიდეებია, ხოლო a₁,a₂,...,a_n-მოცემული სიდიდეები. თუ ამ განტოლებაში a₁=a ≠0 ხოლო a_k=0 (k=2,3,...,n), მივიღებთ ax=b სახის განტოლებას, რომელსაც ერთუცნობიანი წრფივი განტოლება ეწოდება. აქ x - უცნობია, ხოლო a და b - ნებისმიერი ნამდვილი რიცხვები. თუ a ≠ 0, მაშინ განტოლებას ერთადერთი ამონახსნი ქვს: x= a/b; თუ a=0 და b≠0, მაშინ განტოლებას ამონახსნი არა აქვს, ხოლო თუ a=0 და b=0, მაშინ განტოლებას აქვს უსასრულოდ ბევრი ამონახსნი.

ვთქვათ მოცემულია n წრფივ განტოლებათა სისტემა n უცნობით:

წრფივ განტოლებათა სისტემას შეიძლება ჰქონდეს როგორც ერთადერთი, ასევე უამრავი ამონახსნი, ან საერთოდ არა ჰქონდეს ამონახსნი. თუ განტოლებათა რიცხვი უცნობთა რიცხვის ტოლია. n - უცნობიან n განტოლებათა სისტემას ყოველთვის აქვს ამონახსნი, თუ სისტემის D დეტერმინანტი განსხვავდება ნულისაგან (D≠0).

ასეთ სისტემათა ამონახსნი მიიღება კრამერის წესით.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი