ინტეგრალი მრუდწირული
მ (მომხმარებელმა Echelidze გვერდი „ინტეგრალი მრუდწირული“ გადაიტანა გვერდზე „[[მრუდწირული ინტეგრალი]...) |
|||
| (ერთი მომხმარებლის 2 შუალედური ვერსიები არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
| − | '''ინტეგრალი მრუდწირული''' – განსაზღვრული ინტეგრალი რამდენიმე | + | '''ინტეგრალი მრუდწირული''' – [[განსაზღვრული ინტეგრალი]] რამდენიმე [[ცვლადი]]ს [[ფუნქცია (მათემატიკური)|ფუნქციიდან]], რომელშიც [[ინტეგრება]] ხდება [[წირი|წირის]] მოცემულ [[რკალი (მათემატიკა)|რკალზე]] (1-ლი გვარის მრუდწირული [[ინტეგრალი]]), ან [[საკოორდინატო ღერძი|საკოორდინატო ღერძებზე]] მისი [[გეგმილი (პროექცია)|გეგმილებით]] (მე-2 გვარის მრუდწირული ინტეგრალი). მაგალითად, 1-ლი გვარის მრუდწირული ინტეგრალი ასე აღინიშნება |
| − | :::[[ფაილი:Integrali mrudwiruli001.png]]f(P)ds, სადაც Г – მოცემული წირია, ds- მისი რკალის დიფერენციალი, f(P) – წირზე აღებული წერტილის ფუნქცია. | + | :::[[ფაილი:Integrali mrudwiruli001.png]]f(P)ds, სადაც Г – მოცემული წირია, ds- მისი რკალის [[დიფერენციალი]], f(P) – წირზე აღებული [[წერტილი (გეომეტრია)|წერტილის]] ფუნქცია. |
| − | მე-2 გვარის მრუდწირული ინტეგრალი წარმოიშობა, მაგალითად, ძალთა | + | მე-2 გვარის მრუდწირული ინტეგრალი წარმოიშობა, მაგალითად, [[ძალთა ველი]]ს მუშაობის [[ამოცანა (მათემატიკა)|ამოცანის]] განხილვისას; [[ბრტყელი წირი|ბრტყელი Г წირი]]სათვის ასე ჩაიწერება: |
:::[[ფაილი:Integrali mrudwiruli001.png]]P(x,y)dx + Q(x,y)dy, | :::[[ფაილი:Integrali mrudwiruli001.png]]P(x,y)dx + Q(x,y)dy, | ||
| − | სივრცითი Г | + | [[სივრცითი წირი|სივრცითი Г წირი]]სათვის [[ფაილი:Integrali mrudwiruli001.png]]P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz. |
მრუდწირული ინტეგრალი წარმოადგენს ჩვეულებრივი ინტეგრალის განზოგადებას და გააჩნია მისი ყველა თვისება. | მრუდწირული ინტეგრალი წარმოადგენს ჩვეულებრივი ინტეგრალის განზოგადებას და გააჩნია მისი ყველა თვისება. | ||
| − | მრუდწირული ინტეგრალი პირველად გვხვდება კლეროს შრომაში (1743). იქვეა მოყვანილი ინტეგრების გზისაგან დამოუკიდებლობის პირობა. ზოგადი სახით მრუდწირული ინტეგრალები შემოიღო კოშიმ თავის შრომებში კომპლექსური ცვლადის ფუნქციების შესახებ (1825). გამოთქმა „ინტეგრების გზა“ მრუდწირული ინტეგრალებისათვის შემოიღო ფრანგმა მათემატიკოსმა პიუიზემ (1850). ნიშანი ∮, რომელიც მიუთითებს, რომ ინტეგრალი აღებულია ჩაკეტილი | + | მრუდწირული ინტეგრალი პირველად გვხვდება კლეროს შრომაში (1743). იქვეა მოყვანილი ინტეგრების გზისაგან დამოუკიდებლობის [[პირობა (მათემატიკა)|პირობა]]. ზოგადი სახით მრუდწირული ინტეგრალები შემოიღო კოშიმ თავის შრომებში [[კომპლექსური ცვლადის ფუნქცია|კომპლექსური ცვლადის ფუნქციების]] შესახებ (1825). გამოთქმა „ინტეგრების გზა“ მრუდწირული ინტეგრალებისათვის შემოიღო ფრანგმა მათემატიკოსმა პიუიზემ (1850). ნიშანი ∮, რომელიც მიუთითებს, რომ ინტეგრალი აღებულია ჩაკეტილი [[კონტური |კონტური]]ს გასწვრივ, შემოიღო კრამერსმა (1923). |
| ხაზი 18: | ხაზი 18: | ||
[[კატეგორია:ალგებრა]] | [[კატეგორია:ალგებრა]] | ||
[[კატეგორია:მათემატიკა]] | [[კატეგორია:მათემატიკა]] | ||
| + | [[კატეგორია:ინტეგრალები]] | ||
მიმდინარე ცვლილება 22:08, 6 ივლისი 2024 მდგომარეობით
ინტეგრალი მრუდწირული – განსაზღვრული ინტეგრალი რამდენიმე ცვლადის ფუნქციიდან, რომელშიც ინტეგრება ხდება წირის მოცემულ რკალზე (1-ლი გვარის მრუდწირული ინტეგრალი), ან საკოორდინატო ღერძებზე მისი გეგმილებით (მე-2 გვარის მრუდწირული ინტეგრალი). მაგალითად, 1-ლი გვარის მრუდწირული ინტეგრალი ასე აღინიშნება
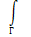f(P)ds, სადაც Г – მოცემული წირია, ds- მისი რკალის დიფერენციალი, f(P) – წირზე აღებული წერტილის ფუნქცია.
მე-2 გვარის მრუდწირული ინტეგრალი წარმოიშობა, მაგალითად, ძალთა ველის მუშაობის ამოცანის განხილვისას; ბრტყელი Г წირისათვის ასე ჩაიწერება:
- P(x,y)dx + Q(x,y)dy,
სივრცითი Г წირისათვის 
P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz.
მრუდწირული ინტეგრალი წარმოადგენს ჩვეულებრივი ინტეგრალის განზოგადებას და გააჩნია მისი ყველა თვისება.
მრუდწირული ინტეგრალი პირველად გვხვდება კლეროს შრომაში (1743). იქვეა მოყვანილი ინტეგრების გზისაგან დამოუკიდებლობის პირობა. ზოგადი სახით მრუდწირული ინტეგრალები შემოიღო კოშიმ თავის შრომებში კომპლექსური ცვლადის ფუნქციების შესახებ (1825). გამოთქმა „ინტეგრების გზა“ მრუდწირული ინტეგრალებისათვის შემოიღო ფრანგმა მათემატიკოსმა პიუიზემ (1850). ნიშანი ∮, რომელიც მიუთითებს, რომ ინტეგრალი აღებულია ჩაკეტილი კონტურის გასწვრივ, შემოიღო კრამერსმა (1923).
