ლაპლასის ოპერატორი
მ (მომხმარებელმა Echelidze გვერდი „ლაპლასიანი“ გადაიტანა გვერდზე „ლაპლასის ოპერატორი“ გადამისამ...) |
|||
| ხაზი 1: | ხაზი 1: | ||
| − | '''ლაპლასის ოპერატორი''' (ლაპლასიანი, ანუ დელტა-ოპერატორი) – მეორე რიგის წრფივი დიფერენციალური ოპერატორი, რომელიც აღინიშნება ∆ (დელტა) ან ∇<sup>2</sup> სიმბოლოთი: | + | '''ლაპლასის ოპერატორი''' (ლაპლასიანი, ანუ [[დელტა ოპერატორი|დელტა-ოპერატორი]]) – მეორე რიგის წრფივი [[დიფერენციალი|დიფერენციალური]] [[ოპერატორი (მათემატიკა)|ოპერატორი]], რომელიც აღინიშნება ∆ (დელტა) ან ∇<sup>2</sup> [[სიმბოლო|სიმბოლოთი]]: |
:::[[ფაილი:Laplasis operatori005.png]] | :::[[ფაილი:Laplasis operatori005.png]] | ||
| − | :::აქ [[ფაილი:Laplasis operatori007.png]] – ჰამილტონის | + | :::აქ [[ფაილი:Laplasis operatori007.png]] – [[ჰამილტონის ოპერატორი]]ა. |
| − | თუ φ არის n ცვლადის ორჯერ წარმოებადი ფუნქცია φ=φ(x<sub>1</sub>,x<sub>2</sub>,…,x<sub>n</sub>), მაშინ | + | თუ φ არის n [[ცვლადი|ცვლადის]] ორჯერ წარმოებადი [[ფუნქცია (მათემატიკური)|ფუნქცია]] φ=φ(x<sub>1</sub>,x<sub>2</sub>,…,x<sub>n</sub>), მაშინ |
:::[[ფაილი:Laplasis operatori015.png]] | :::[[ფაილი:Laplasis operatori015.png]] | ||
| ხაზი 16: | ხაზი 16: | ||
| − | თუ ვექტორული ველი პოტენციურია, მაშინ div (grad u) = 0 და მაშასადამე, პოტენციური ფუნქცია u – ჰარმონიულია, ვინაიდან ის აკმაყოფილებს ლაპლასის | + | თუ [[ვექტორული ველი]] [[პოტენციალი (მათემატიკური)|პოტენციურია]], მაშინ div (grad u) = 0 და მაშასადამე, პოტენციური ფუნქცია u – [[ჰარმონიული ფუნქცია|ჰარმონიულია]], ვინაიდან ის აკმაყოფილებს [[ლაპლასის განტოლება]]ს: |
| ხაზი 22: | ხაზი 22: | ||
| − | :ლაპლასის ოპერატორი ცილინდრულ კოორდინატებში: | + | :[[ლაპლასი პიერ სიმონ|ლაპლასის]] ოპერატორი [[ცილინდრული კოორდინატები|ცილინდრულ კოორდინატებში]]: |
| ხაზი 28: | ხაზი 28: | ||
| − | ლაპლასის ოპერატორი მნიშვნელოვან როლს თამაშობს მათემატიკურ ანალიზში, მათემატიკურ ფიზიკაში, | + | ლაპლასის ოპერატორი მნიშვნელოვან როლს თამაშობს [[მათემატიკური ანალიზი|მათემატიკურ ანალიზში]], [[მათემატიკური ფიზიკა|მათემატიკურ ფიზიკაში]], [[გეომეტრია]]ში. |
| − | ლაპლასის ოპერატორის მნიშვნელობა მათემატიკის მრავალ საკითხში განპირობებულია მისი ძირითადი თვისებით: ეს ოპერატორი წარმოადგენს ერთადერთს მეორე რიგის ყველა დიფერენციალურ ოპერატორს შორის, რომელიც ინვარიანტულია x<sub>1</sub>,x<sub>2</sub>,…,x<sub>n</sub> ცვლადების ნებისმიერი ორთოგონალური გარდაქმნის მიმართ. | + | ლაპლასის ოპერატორის მნიშვნელობა [[მათემატიკა|მათემატიკის]] მრავალ საკითხში განპირობებულია მისი ძირითადი თვისებით: ეს ოპერატორი წარმოადგენს ერთადერთს მეორე რიგის ყველა დიფერენციალურ ოპერატორს შორის, რომელიც [[ინვარიანტი|ინვარიანტულია]] x<sub>1</sub>,x<sub>2</sub>,…,x<sub>n</sub> ცვლადების ნებისმიერი [[ორთოგონალური გარდაქმნა|ორთოგონალური გარდაქმნის]] მიმართ. |
მიმდინარე ცვლილება 19:28, 16 მარტი 2024 მდგომარეობით
ლაპლასის ოპერატორი (ლაპლასიანი, ანუ დელტა-ოპერატორი) – მეორე რიგის წრფივი დიფერენციალური ოპერატორი, რომელიც აღინიშნება ∆ (დელტა) ან ∇2 სიმბოლოთი:
- აქ
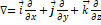– ჰამილტონის ოპერატორია.
- აქ
თუ φ არის n ცვლადის ორჯერ წარმოებადი ფუნქცია φ=φ(x1,x2,…,xn), მაშინ
- განვიხილოთ
თუ ვექტორული ველი პოტენციურია, მაშინ div (grad u) = 0 და მაშასადამე, პოტენციური ფუნქცია u – ჰარმონიულია, ვინაიდან ის აკმაყოფილებს ლაპლასის განტოლებას:
(ანუ ∆ u =0).
:ლაპლასის ოპერატორი ცილინდრულ კოორდინატებში:
ლაპლასის ოპერატორი მნიშვნელოვან როლს თამაშობს მათემატიკურ ანალიზში, მათემატიკურ ფიზიკაში, გეომეტრიაში.
ლაპლასის ოპერატორის მნიშვნელობა მათემატიკის მრავალ საკითხში განპირობებულია მისი ძირითადი თვისებით: ეს ოპერატორი წარმოადგენს ერთადერთს მეორე რიგის ყველა დიფერენციალურ ოპერატორს შორის, რომელიც ინვარიანტულია x1,x2,…,xn ცვლადების ნებისმიერი ორთოგონალური გარდაქმნის მიმართ.
