მეორე რიგის წირები
მ (მომხმარებელმა Echelidze გვერდი „წირი მეორე რიგის“ გადაიტანა გვერდზე „მეორე რიგის წირები“ გადამ...) |
|||
| ხაზი 5: | ხაზი 5: | ||
:::ან (a<sub>11</sub>x + a<sub>12</sub>y + a<sub>13</sub>)x + (a<sub>21</sub>x + a<sub>22</sub>y + a<sub>23</sub>)y + (a<sub>31</sub>x + a<sub>32</sub>y + a<sub>33</sub>) = 0 | :::ან (a<sub>11</sub>x + a<sub>12</sub>y + a<sub>13</sub>)x + (a<sub>21</sub>x + a<sub>22</sub>y + a<sub>23</sub>)y + (a<sub>31</sub>x + a<sub>32</sub>y + a<sub>33</sub>) = 0 | ||
| − | სადაც a<sub>11</sub>,a<sub>12</sub>,a<sub>22</sub> – ნამდვილი | + | სადაც a<sub>11</sub>,a<sub>12</sub>,a<sub>22</sub> – [[ნამდვილი რიცხვები]]ა, რომლებიც ერთდროულად არ არიან [[ნული]]ს [[ტოლობა|ტოლნი]], ამასთანავე a<sub>ik</sub> = a<sub>ki</sub> (i, k = 1, 2, 3). |
| − | ნებისმიერი ('''*''') განტოლებისათვის სამი სიდიდე – I, D, A, წარმოადგენს ინვარიანტულს კოორდინატთა ღერძების გადატანისა და მობრუნების მიმართ, სადაც | + | ნებისმიერი ('''*''') [[განტოლება|განტოლებისათვის]] სამი [[სიდიდე (მათემატიკა)|სიდიდე]] – I, D, A, წარმოადგენს [[ინვარიანტი|ინვარიანტულს]] [[ღერძი საკოორდინატო|კოორდინატთა ღერძების]] გადატანისა და მობრუნების მიმართ, სადაც |
:::::[[ფაილი:Meore009.png]] | :::::[[ფაილი:Meore009.png]] | ||
| − | ეს ინვარიანტები განსაზღვრავენ მეორე რიგის | + | ეს ინვარიანტები განსაზღვრავენ მეორე რიგის [[წირი]]ს თვისებებს, დამოუკიდებლად [[სიბრტყე (გეომეტრია)|სიბრტყეზე]] მათი მდებარეობისა. |
| − | A ინვარიანტს აგრეთვე უწოდებენ ('''*''') განტოლების დისკრიმინანტს. | + | A ინვარიანტს აგრეთვე უწოდებენ ('''*''') განტოლების [[დისკრიმინანტი|დისკრიმინანტს]]. |
| − | მეორე რიგის წირებია: წრეწირი, ელიფსი, ჰიპერბოლა და პარაბოლა, რომლებიც ჯერ კიდევ ანტიკური ხანის მათემატიკოსებმა შეისწავლეს. ამ წირებს ზოგჯერ კონუსური კვეთის წირებს უწოდებენ. | + | მეორე რიგის წირებია: [[წრეწირი]], [[ელიფსი]], [[ჰიპერბოლა]] და [[პარაბოლა]], რომლებიც ჯერ კიდევ ანტიკური ხანის მათემატიკოსებმა შეისწავლეს. ამ წირებს ზოგჯერ [[კონუსური კვეთები|კონუსური კვეთის]] წირებს უწოდებენ. |
| − | კოორდინატთა მართკუთხა სისტემაში ('''*''') განტოლება კოეფიციენტების მიხედვით დაიყვანება შემდეგი ცხრა კანონიკური სახიდან ერთ-ერთზე, რომელთაგან თითოეულს შეესაბამება მეორე რიგის წირების გარკვეული კლასი. | + | [[დეკარტის კოორდინატთა სისტემა|კოორდინატთა მართკუთხა სისტემაში]] ('''*''') განტოლება [[კოეფიციენტი (მათემატიკა)|კოეფიციენტების]] მიხედვით დაიყვანება შემდეგი ცხრა [[კანონიკა|კანონიკური]] სახიდან ერთ-ერთზე, რომელთაგან თითოეულს შეესაბამება მეორე რიგის წირების გარკვეული კლასი. |
::'''I. არადაშლადი წირები:''' | ::'''I. არადაშლადი წირები:''' | ||
| − | :::[[ფაილი:Meore011.png]] – ელიფსი, | + | :::[[ფაილი:Meore011.png]] – [[ელიფსი]], |
| − | :::[[ფაილი:Meore013.png]] – ჰიპერბოლა, | + | :::[[ფაილი:Meore013.png]] – [[ჰიპერბოლა]], |
| − | :::y = 2px<sup>2</sup> – პარაბოლა, | + | :::y = 2px<sup>2</sup> – [[პარაბოლა]], |
| ხაზი 35: | ხაზი 35: | ||
:::[[ფაილი:Meore019.png]] – გადამკვეთ წრფეთა წყვილი, | :::[[ფაილი:Meore019.png]] – გადამკვეთ წრფეთა წყვილი, | ||
| − | :::[[ფაილი:Meore021.png]] – წარმოსახვით გადამკვეთ | + | :::[[ფაილი:Meore021.png]] – წარმოსახვით გადამკვეთ [[წრფე]]თა წყვილი, |
| − | :::x<sup>2</sup> – a<sup>2</sup> = 0 – პარალელურ წრფეთა წყვილი, | + | :::x<sup>2</sup> – a<sup>2</sup> = 0 – [[პარალელური წრფეები|პარალელურ წრფეთა]] წყვილი, |
| − | :::x<sup>2</sup> + a<sup>2</sup> = 0 – წარმოსახვით პარალელურ | + | :::x<sup>2</sup> + a<sup>2</sup> = 0 – წარმოსახვით პარალელურ [[წრფე]]თა წყვილი, |
:::x<sup>2</sup> = 0 – თანამთხვევადი წრფეთა წყვილი. | :::x<sup>2</sup> = 0 – თანამთხვევადი წრფეთა წყვილი. | ||
| − | მეორე რიგის წირებს, რომელთაც აქვთ ერთადერთი სიმეტრიის ცენტრი, ეწოდებათ მეორე რიგის ცენტრალური წირები. | + | მეორე რიგის წირებს, რომელთაც აქვთ ერთადერთი [[სიმეტრიის ცენტრი]], ეწოდებათ მეორე რიგის ცენტრალური წირები. |
| − | კონუსური კვეთები ცნობილი იყო ჯერ კიდევ ძველი | + | [[კონუსური კვეთები]] ცნობილი იყო ჯერ კიდევ ძველი [[საბერძნეთი]]ს მათემატიკოსებისათვის. ყველაზე სრული თხზულება, რომელიც მიეძღვნა ამგვარ წირებს, იყო [[აპოლონიოს პერგასელი|აპოლონიოს პერგელი]]ს „კონუსური კვეთები“ (დაახლ. ძვ. წ. 200 წ.). |
| − | ბერძენი მათემატიკოსების მიერ კონუსური კვეთების შესწავლისას მიღებული მნიშვნელოვანი შედეგების შემდეგ დადგა დიდი ხნის შესვენება. 12 საუკუნის განმავლობაში არ ყოფილა არც ერთი საყურადღებო აღმოჩენა. მხოლოდ 1522 წ-ს გადაიდგა მნიშვნელოვანი ნაბიჯი, როდესაც ნიურნბერგელმა ი. ვერნერმა წრეწირის დაგეგმილებისას აღმოაჩინა კონუსური კვეთების რამდენიმე ახალი მნიშვნელოვანი თვისება. აღმოჩენების ნაკადი დაიწყო ანალიზური გეომეტრიის შექმნის შემდეგ. პირველ ნაშრომს, რომელშიც წირები განიხილებიან არა როგორც კონუსური კვეთები, არამედ, როგორც მეორე რიგის წირები და მათი კვლევა ხდება დეკარტის საკოორდინატო მეთოდით, ეწოდებოდა „ტრაქტატი კონუსური კვეთების შესახებ, გადმოცემული ახალი ხერხით“ (1655). ვალისის ამ ტრაქტატში ახალი იყო მხოლოდ გადმოცემის ფორმა, არაფერი სხვა, გარდა იმისა, რაც ცნობილი იყო ჯერ კიდევ აპოლონიისათვის, აქ არ შედის. სახელწოდება იმით იყო განპირობებული, რომ ამ წირების განტოლებებში ცვლადები შედიან მეორე ხარისხში. | + | ბერძენი მათემატიკოსების მიერ კონუსური კვეთების შესწავლისას მიღებული მნიშვნელოვანი შედეგების შემდეგ დადგა დიდი ხნის შესვენება. 12 საუკუნის განმავლობაში არ ყოფილა არც ერთი საყურადღებო აღმოჩენა. მხოლოდ 1522 წ-ს გადაიდგა მნიშვნელოვანი ნაბიჯი, როდესაც ნიურნბერგელმა ი. ვერნერმა წრეწირის დაგეგმილებისას აღმოაჩინა კონუსური კვეთების რამდენიმე ახალი მნიშვნელოვანი თვისება. აღმოჩენების ნაკადი დაიწყო [[ანალიზური გეომეტრია|ანალიზური გეომეტრიის]] შექმნის შემდეგ. პირველ ნაშრომს, რომელშიც წირები განიხილებიან არა როგორც კონუსური კვეთები, არამედ, როგორც მეორე რიგის წირები და მათი კვლევა ხდება [[დეკარტის კოორდინატები|დეკარტის საკოორდინატო მეთოდით]], ეწოდებოდა „ტრაქტატი კონუსური კვეთების შესახებ, გადმოცემული ახალი ხერხით“ (1655). [[ვალისი ჯონი|ვალისის]] ამ [[ტრაქტატი|ტრაქტატში]] ახალი იყო მხოლოდ გადმოცემის ფორმა, არაფერი სხვა, გარდა იმისა, რაც ცნობილი იყო ჯერ კიდევ [[აპოლონ პერგელი (აპოლონიოს პერგასელი)|აპოლონიისათვის]], აქ არ შედის. სახელწოდება იმით იყო განპირობებული, რომ ამ წირების განტოლებებში [[ცვლადი|ცვლადები]] შედიან მეორე ხარისხში. |
| − | მალე პირველად იქნა ანალიზურად გამოყვანილი ელიფსისა და ჰიპერბოლის განტოლება, როგორც წერტილთა გეომეტრიული ადგილი, რომელთათვისაც სრულდება პირობები MF<sub>1</sub> + MF<sub>2</sub>=2a და MF<sub>1</sub>-MF<sub>2</sub>=2a. ასეთი გადმოცემა ჩაატარა ვან სხოუტენის მოწაფემ იან დე ვიტმა, რომელიც გარკვეული დროის განმავლობაში ჰოლანდიის (ნიდერლანდების) | + | მალე პირველად იქნა ანალიზურად გამოყვანილი ელიფსისა და ჰიპერბოლის განტოლება, როგორც წერტილთა [[გეომეტრიული ადგილი]], რომელთათვისაც სრულდება [[პირობა (მათემატიკა)|პირობები]] MF<sub>1</sub> + MF<sub>2</sub>=2a და MF<sub>1</sub>-MF<sub>2</sub>=2a. ასეთი გადმოცემა ჩაატარა ვან სხოუტენის მოწაფემ იან დე ვიტმა, რომელიც გარკვეული დროის განმავლობაში ჰოლანდიის ([[ნიდერლანდები|ნიდერლანდების]]) [[სახელმწიფო]]ს მეთაური იყო. მისი „მრუდე წირების საწყისები“ დაბეჭდილია [[დეკარტი რენე|დეკარტი]]ს „გეომეტრიის“ მეორე გამოცემაში (1659-1661). ჰიპერბოლის განტოლება xy=k სახით პირველად გვხვდება [[ფერმა პიერ|ფერმასთან]] (1659), თვისება კი MF<sub>1</sub>-MF<sub>2</sub>=2a აპოლონიისაც აქვს. |
| − | კონუსური კვეთების განსაზღვრა ფოკუსის და დირექტრისის საშუალებით, როგორც ჩანს, | + | კონუსური კვეთების განსაზღვრა [[ფოკუსი|ფოკუსის]] და [[დირექტრისა|დირექტრისის]] საშუალებით, როგორც ჩანს, [[ევკლიდე]]სთვის ცნობილი იყო, იგი პაპსაც აქვს. სახელწოდება „დირექტრისა“ (პარაბოლისათვის) შემოიღო ლოპიტალმა. |
| − | + | [[არქიმედე]]მ გამოთვალა პარაბოლური [[სეგმენტი (მათემატიკა)|სეგმენტის]] [[ფართობი (გეომეტრია)|ფართობი]], ამასთანავე, იპოვა ელიფსის ფართობის [[ფორმულა]] πab, სადაც იგი უშვებდა, რომ [[ფაილი:Meore035.png]]. სენ ვინსეტმა მონახა ფორმულა ჰიპერბოლის [[რკალი (მათემატიკა)|რკალსა]] და [[ასიმპტოტი|ასიმპტოტს]] შორის ფართობის გამოსათვლელად. მაქსველმა შრომაში „ტრაქტატი ფლუქსიების შესახებ“ (1742) კონუსური კვეთის [[რკალის სიგრძე]] წარმოადგინა [[ინტეგრალი|ინტეგრალის]] სახით. ლენდენმა აღმოაჩინა, რომ ჰიპერბოლის ნებისმიერი რკალი შეიძლება გამოვსახოთ ორი ელიფსის რკალის [[სიგრძე (მათემატიკა)|სიგრძით]]. კონუსური კვეთების რკალების შესახებ მრავალი [[თეორემა]] მიიღო ფანიანომ (1716), ხოლო შემდგომში [[ეილერი ლეონარდ|ეილერმა]] (1736, გამოქვეყნებულია 1741). თითქმის ერთდროულად იქნა მოძებნილი ელიფსის სიგრძის მიახლოებითი საანგარიშო ფორმულა 4q= π{α+b+0,5(√<span style="box-sizing: border-box;tures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; ohans: 2; text-align: center; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; text-decoration: overline">α</span> – √<span style="box-sizing: border-box;tures: normal; font-variant-caps: normal; font-weight: 400; letter-spacing: normal; ohans: 2; text-align: center; text-indent: 0px; text-transform: none; white-space: normal; widows: 2; word-spacing: 0px; -webkit-text-stroke-width: 0px; text-decoration: overline">b</span>)<sup>2</sup> } პეანოსა (1887) და ბუსინესკის (1889) მიერ. | |
| − | კონუსური კვეთების თეორიისადმი ახალი მიდგომა და შემდგომი განვითარება დაკავშირებულია შტაინერისა (1832) და შტაუდტის (1847) სახელებთან | + | კონუსური კვეთების თეორიისადმი ახალი მიდგომა და შემდგომი განვითარება დაკავშირებულია შტაინერისა (1832) და შტაუდტის (1847) სახელებთან. |
==წყარო== | ==წყარო== | ||
მიმდინარე ცვლილება 17:20, 16 აპრილი 2024 მდგომარეობით
მეორე რიგის წირები – ბრტყელი წირი, რომლის წერტილების დეკარტის კოორდინატები აკმაყოფილებენ მე-2 ხარისხის ალგებრულ განტოლებას:
- a11x2 + 2a12xy + a22y2 + 2a13x + 2a23y + a33 = 0,(*)
- ან (a11x + a12y + a13)x + (a21x + a22y + a23)y + (a31x + a32y + a33) = 0
სადაც a11,a12,a22 – ნამდვილი რიცხვებია, რომლებიც ერთდროულად არ არიან ნულის ტოლნი, ამასთანავე aik = aki (i, k = 1, 2, 3).
ნებისმიერი (*) განტოლებისათვის სამი სიდიდე – I, D, A, წარმოადგენს ინვარიანტულს კოორდინატთა ღერძების გადატანისა და მობრუნების მიმართ, სადაც
ეს ინვარიანტები განსაზღვრავენ მეორე რიგის წირის თვისებებს, დამოუკიდებლად სიბრტყეზე მათი მდებარეობისა.
A ინვარიანტს აგრეთვე უწოდებენ (*) განტოლების დისკრიმინანტს.
მეორე რიგის წირებია: წრეწირი, ელიფსი, ჰიპერბოლა და პარაბოლა, რომლებიც ჯერ კიდევ ანტიკური ხანის მათემატიკოსებმა შეისწავლეს. ამ წირებს ზოგჯერ კონუსური კვეთის წირებს უწოდებენ.
კოორდინატთა მართკუთხა სისტემაში (*) განტოლება კოეფიციენტების მიხედვით დაიყვანება შემდეგი ცხრა კანონიკური სახიდან ერთ-ერთზე, რომელთაგან თითოეულს შეესაბამება მეორე რიგის წირების გარკვეული კლასი.
- I. არადაშლადი წირები:
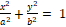– ელიფსი,
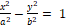– ჰიპერბოლა,
- y = 2px2 – პარაბოლა,
- II. დაშლადი წირები:
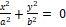– წარმოსახვითი ელიფსი.
– გადამკვეთ წრფეთა წყვილი,
– წარმოსახვით გადამკვეთ წრფეთა წყვილი,
- x2 – a2 = 0 – პარალელურ წრფეთა წყვილი,
- x2 + a2 = 0 – წარმოსახვით პარალელურ წრფეთა წყვილი,
- x2 = 0 – თანამთხვევადი წრფეთა წყვილი.
მეორე რიგის წირებს, რომელთაც აქვთ ერთადერთი სიმეტრიის ცენტრი, ეწოდებათ მეორე რიგის ცენტრალური წირები.
კონუსური კვეთები ცნობილი იყო ჯერ კიდევ ძველი საბერძნეთის მათემატიკოსებისათვის. ყველაზე სრული თხზულება, რომელიც მიეძღვნა ამგვარ წირებს, იყო აპოლონიოს პერგელის „კონუსური კვეთები“ (დაახლ. ძვ. წ. 200 წ.).
ბერძენი მათემატიკოსების მიერ კონუსური კვეთების შესწავლისას მიღებული მნიშვნელოვანი შედეგების შემდეგ დადგა დიდი ხნის შესვენება. 12 საუკუნის განმავლობაში არ ყოფილა არც ერთი საყურადღებო აღმოჩენა. მხოლოდ 1522 წ-ს გადაიდგა მნიშვნელოვანი ნაბიჯი, როდესაც ნიურნბერგელმა ი. ვერნერმა წრეწირის დაგეგმილებისას აღმოაჩინა კონუსური კვეთების რამდენიმე ახალი მნიშვნელოვანი თვისება. აღმოჩენების ნაკადი დაიწყო ანალიზური გეომეტრიის შექმნის შემდეგ. პირველ ნაშრომს, რომელშიც წირები განიხილებიან არა როგორც კონუსური კვეთები, არამედ, როგორც მეორე რიგის წირები და მათი კვლევა ხდება დეკარტის საკოორდინატო მეთოდით, ეწოდებოდა „ტრაქტატი კონუსური კვეთების შესახებ, გადმოცემული ახალი ხერხით“ (1655). ვალისის ამ ტრაქტატში ახალი იყო მხოლოდ გადმოცემის ფორმა, არაფერი სხვა, გარდა იმისა, რაც ცნობილი იყო ჯერ კიდევ აპოლონიისათვის, აქ არ შედის. სახელწოდება იმით იყო განპირობებული, რომ ამ წირების განტოლებებში ცვლადები შედიან მეორე ხარისხში.
მალე პირველად იქნა ანალიზურად გამოყვანილი ელიფსისა და ჰიპერბოლის განტოლება, როგორც წერტილთა გეომეტრიული ადგილი, რომელთათვისაც სრულდება პირობები MF1 + MF2=2a და MF1-MF2=2a. ასეთი გადმოცემა ჩაატარა ვან სხოუტენის მოწაფემ იან დე ვიტმა, რომელიც გარკვეული დროის განმავლობაში ჰოლანდიის (ნიდერლანდების) სახელმწიფოს მეთაური იყო. მისი „მრუდე წირების საწყისები“ დაბეჭდილია დეკარტის „გეომეტრიის“ მეორე გამოცემაში (1659-1661). ჰიპერბოლის განტოლება xy=k სახით პირველად გვხვდება ფერმასთან (1659), თვისება კი MF1-MF2=2a აპოლონიისაც აქვს.
კონუსური კვეთების განსაზღვრა ფოკუსის და დირექტრისის საშუალებით, როგორც ჩანს, ევკლიდესთვის ცნობილი იყო, იგი პაპსაც აქვს. სახელწოდება „დირექტრისა“ (პარაბოლისათვის) შემოიღო ლოპიტალმა.
არქიმედემ გამოთვალა პარაბოლური სეგმენტის ფართობი, ამასთანავე, იპოვა ელიფსის ფართობის ფორმულა πab, სადაც იგი უშვებდა, რომ 
. სენ ვინსეტმა მონახა ფორმულა ჰიპერბოლის რკალსა და ასიმპტოტს შორის ფართობის გამოსათვლელად. მაქსველმა შრომაში „ტრაქტატი ფლუქსიების შესახებ“ (1742) კონუსური კვეთის რკალის სიგრძე წარმოადგინა ინტეგრალის სახით. ლენდენმა აღმოაჩინა, რომ ჰიპერბოლის ნებისმიერი რკალი შეიძლება გამოვსახოთ ორი ელიფსის რკალის სიგრძით. კონუსური კვეთების რკალების შესახებ მრავალი თეორემა მიიღო ფანიანომ (1716), ხოლო შემდგომში ეილერმა (1736, გამოქვეყნებულია 1741). თითქმის ერთდროულად იქნა მოძებნილი ელიფსის სიგრძის მიახლოებითი საანგარიშო ფორმულა 4q= π{α+b+0,5(√α – √b)2 } პეანოსა (1887) და ბუსინესკის (1889) მიერ.
კონუსური კვეთების თეორიისადმი ახალი მიდგომა და შემდგომი განვითარება დაკავშირებულია შტაინერისა (1832) და შტაუდტის (1847) სახელებთან.
