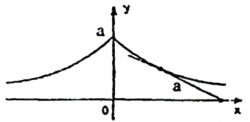
ტრაქტრისა

ტრაქტრისა (სახელწოდება „ტრაქტრისა“ სავსებით გამართლებულია. ლათინური traho – „თრევა“, „წევა“, tractrice – „გამწევი“; ტრაქტრისა – „მიზიდვის წირი“; tractus – „გაჭიმული“, „გაწელილი“) – ბრტყელი წირი, რომლის განტოლება დეკარტის მართკუთხა კოორდინატებში. თუ საბაზისო ღერძია 0x ღერძი, ასეთი სახისაა:

x = ± {α In[(α + ) / y] - }, სადაც α > 0, 0 < y ≤ α;

ხოლო პარამეტრული განტოლება ასეთია:

x = a (ln tg + cost), y = a sint;

t – მხების დახრის კუთხეა 0x ღერძისადმი.

ტრაქტრისა ტრანსცენდენტური წირია; იგი არის ჯაჭვწირის ევოლვენტა.

ტრაქტრისას მახასიათებელი თვისება იმაში მდგომარეობს, რომ მისი მხების მონაკვეთის სიგრძე |MN|=α შეხების M წერტილიდან რაიმე წრფემდე (ვთქვათ, 0x ღერძამდე) მუდმივი სიდიდეა. ამ წრფეს ტრაქტრისას ღერძი ეწოდება. ეს ღერძი არის ტრაქტრისას ასიმპტოტი. ტრაქტრისა სიმეტრიულია 0y ღერძის მიმართ.

ტრაქტრისას სიმრუდის რადიუსი R = a ctg ;

ტრაქტრისით და მისი ასიმპტოტით შემოსაზღვრული ფართობი

ტრაქტრისას ბრუნვით მისი 0x ღერძის გარშემო მიიღება ზედაპირი, რომელსაც ფსევდოსფერო ეწოდება.

1675 წელს კლაუდიო პერომ თავის ერთ-ერთ სტატიაში დასვა ამოცანა: მოიძებნოს წირი, რომელზეც გადაადგილდება ჰორიზონტალურ სიბრტყეში მდებარე M წერტილი, რომელიც მიმაგრებულია უჭიმადი ძაფის ბოლოზე, თუ ამ ძაფის მეორე (N) ბოლო გადაადგილდება იმავე სიბრტყეში მდებარე რაიმე (ვთქვათ 0x) წრფის გასწვრივ. ამ წირს ტრაქტრისა ეწოდება. კ. პერო იყო ცნობილი არქიტექტორი, რომელმაც ლუვრში დააგეგმარა „პეროს კოლონადა“; გარდა ამისა, იგი იყო მრავალმხრივ განათლებული პიროვნება: ექიმი, ნატურალისტი, ფიზიკოსი, კონსტრუქტორი, მექანიკოსი, არქეოლოგი.

წირი გამოიკვლიეს ლაიბნიცმა და ჰიუგენსმა (1693). ჰიუგენსმა განაზოგადა ამოცანა; მან დაუშვა, რომ ძაფის ბოლო გადაადგილდება ნებისმიერ წირზე (და არა წრფეზე). ასე წარმოიშვა წრეწირის ტრაქტრისას ცნება, პარაბოლას ტრაქტრისას ცნება და ა. შ.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი