წრფის განტოლება
| ხაზი 7: | ხაზი 7: | ||
| − | '''2) საკუთხო | + | '''2) [[საკუთხო კოეფიციენტი]]თ.''' [[წრფე]] ადგენს φ [[კუთხე (გეომეტრია)|კუთხე]]ს 0x [[ღერძი|ღერძის]] დადებით [[მიმართულება (მათემატიკური)|მიმართულებასთან]] და კვეთს 0y ღერძს (0,b) [[წერტილი (გეომეტრია)|წერტილში]]. |
:::::::::y = kx + b, k = tgφ. (2) | :::::::::y = kx + b, k = tgφ. (2) | ||
| ხაზი 13: | ხაზი 13: | ||
| − | '''3) ღერძთა მონაკვეთებში.''' წრფე კვეთს Ox ღერძს (a,0) წერტილში და 0y ღერძს (0,b) წერტილში: | + | '''3) ღერძთა [[მონაკვეთი (გეომეტრია)|მონაკვეთებში]].''' წრფე კვეთს Ox ღერძს (a,0) წერტილში და 0y ღერძს (0,b) წერტილში: |
:::::::::[[ფაილი:Wrfi021.png]] (a≠0, b≠0). (3) | :::::::::[[ფაილი:Wrfi021.png]] (a≠0, b≠0). (3) | ||
| − | '''4) ნორმალური სახის განტოლება.''' x cos θ + y sinθ - p = 0, (4) | + | '''4) [[ნორმალური განტოლება|ნორმალური სახის განტოლება]].''' x cos θ + y sinθ - p = 0, (4) |
| − | სადაც P – კოორდინატთა სათავიდან წრფეზე დაშვებული პერპენდიკულარის | + | სადაც P – [[კოორდინატთა სათავე|კოორდინატთა სათავიდან]] წრფეზე დაშვებული [[პერპენდიკულარი|პერპენდიკულარის]] [[სიგრძე (მათემატიკა)|სიგრძე]]ა, ხოლო θ – კუთხე 0x ღერძის დადებით მიმართულებასა და პერპენდიკულარს შორის. |
| − | ნორმალური სახის (4) განტოლება შეიძლება მიღებული იქნას ზოგადი სახის (1) განტოლებიდანაც, თუ მას გავამრავლებთ მაინტეგრებელ μ მამრავლზე | + | ნორმალური სახის (4) [[განტოლება]] შეიძლება მიღებული იქნას ზოგადი სახის (1) განტოლებიდანაც, თუ მას [[გამრავლება|გავამრავლებთ]] [[მაინტეგრებელი მამრავლი|მაინტეგრებელ]] μ [[მამრავლი|მამრავლზე]] |
:::::::::[[ფაილი:Wrfi031.png]] | :::::::::[[ფაილი:Wrfi031.png]] | ||
μ -ს და C-ს ნიშნები ურთიერთსაწინააღმდეგო აქვთ. | μ -ს და C-ს ნიშნები ურთიერთსაწინააღმდეგო აქვთ. | ||
| − | თუ წრფის განტოლება მოცემულია ზოგადი სახით, მაშინ არსებობს დამოკიდებულებები: | + | თუ წრფის განტოლება მოცემულია ზოგადი სახით, მაშინ არსებობს [[დამოკიდებულება (მათემატიკური ტერმინი)|დამოკიდებულებები]]: |
:(2)-ში: k = - A/B, φ = θ - π/2, როცა k>0; φ = θ + π/2, როცა k<0. | :(2)-ში: k = - A/B, φ = θ - π/2, როცა k>0; φ = θ + π/2, როცა k<0. | ||
| ხაზი 34: | ხაზი 34: | ||
| − | '''5) წრფეთა კონის განტოლება''' ცენტრით M(x<sub>0</sub>, y<sub>0</sub>) წერტილში: | + | '''5) წრფეთა [[კონა (გეომეტრია)|კონის]] განტოლება''' [[ცენტრი (გეომეტრია)|ცენტრით]] M(x<sub>0</sub>, y<sub>0</sub>) წერტილში: |
:::::::::y - y<sub>0</sub> = k (x - x<sub>0</sub>). (5) | :::::::::y - y<sub>0</sub> = k (x - x<sub>0</sub>). (5) | ||
| ხაზი 43: | ხაზი 43: | ||
| − | '''7) მანძილი M<sub>0</sub> (x<sub>0</sub>, y<sub>0</sub>) წერტილიდან Ax + By + C = 0 წრფემდე:''' | + | '''7) [[მანძილი (გეომეტრია)|მანძილი]] M<sub>0</sub> (x<sub>0</sub>, y<sub>0</sub>) წერტილიდან Ax + By + C = 0 წრფემდე:''' |
:::::::::[[ფაილი:Wrfi059.png]] (7) | :::::::::[[ფაილი:Wrfi059.png]] (7) | ||
| ხაზი 54: | ხაზი 54: | ||
'''8) კუთხე ორ მოცემულ წრფეს შორის:''' | '''8) კუთხე ორ მოცემულ წრფეს შორის:''' | ||
| − | :ა) თუ წრფეთა განტოლებები მოცემულია (1) ფორმით, მაშინ | + | :ა) თუ წრფეთა განტოლებები მოცემულია (1) [[ფორმა (მათემატიკა)|ფორმით]], მაშინ |
:::::::::[[ფაილი:Wrfi065.png]] (8) | :::::::::[[ფაილი:Wrfi065.png]] (8) | ||
| ხაზი 66: | ხაზი 66: | ||
| − | '''10) ორი წრფის პარალელობის პირობა:''' | + | '''10) ორი წრფის პარალელობის [[პირობა (მათემატიკა)|პირობა]]:''' |
:::::::::[[ფაილი:Wrfi073.png]] ან k<sub>1</sub>=k<sub>2</sub>; (10) | :::::::::[[ფაილი:Wrfi073.png]] ან k<sub>1</sub>=k<sub>2</sub>; (10) | ||
| ხაზი 77: | ხაზი 77: | ||
| − | '''12) ზოგადი სახის:''' წრფე, როგორც ორი სიბრტყის თანაკვეთა: | + | '''12) ზოგადი სახის:''' წრფე, როგორც ორი [[სიბრტყე (გეომეტრია)|სიბრტყის]] [[თანაკვეთა]]: |
:::::::::[[ფაილი:Wrfiv081.png]] | :::::::::[[ფაილი:Wrfiv081.png]] | ||
| ხაზი 85: | ხაზი 85: | ||
| − | '''14) მოცემულ M<sub>1</sub>(x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>) წერტილზე გამავალი და მიმმართველი [[ფაილი:Wrfi089.png]] (ℓ, m, n) ვექტორის პარალელური წრფის განტოლება:''' | + | '''14) მოცემულ M<sub>1</sub>(x<sub>1</sub>, y<sub>1</sub>, z<sub>1</sub>) წერტილზე გამავალი და [[მიმმართველი]] [[ფაილი:Wrfi089.png]] (ℓ, m, n) [[ვექტორი|ვექტორის]] [[პარალელური წრფეები|პარალელური წრფის]] განტოლება:''' |
| − | :::::::::[[ფაილი:Wrfi093.png]] (კანონიკური განტოლება), (14) | + | :::::::::[[ფაილი:Wrfi093.png]] ([[კანონიკური განტოლება]]), (14) |
| − | ან x = x<sub>1</sub> + ℓt, y = y<sub>1</sub> + mt, z = z<sub>1</sub> + nt (პარამეტრული განტოლება). | + | ან x = x<sub>1</sub> + ℓt, y = y<sub>1</sub> + mt, z = z<sub>1</sub> + nt ([[პარამეტრი (მათემატიკა)|პარამეტრული]] განტოლება). |
| ხაზი 105: | ხაზი 105: | ||
:::::::::l<sub>1</sub>l<sub>2</sub> + m<sub>1</sub>m<sub>2</sub> + n<sub>1</sub>n<sub>2</sub> = 0. (17) | :::::::::l<sub>1</sub>l<sub>2</sub> + m<sub>1</sub>m<sub>2</sub> + n<sub>1</sub>n<sub>2</sub> = 0. (17) | ||
| − | პირველად პ. ფერმამ (1636) გამოთქვა შენიშვნა, რომ ნებისმიერი პირველი ხარისხის ორი ცვლადის განტოლება არის წრფის განტოლება. ამ ფაქტის დამტკიცება მოგვცა ი. დე ვიტომ (1658-1659). წრფის ნორმალური განტოლება ო. კოშისთან გვხვდება, მაგრამ საყოველთაო ხმარებაში შემოვიდა ო. გესეს გეომეტრიის სახელმძღვანელოს გამოსვლის შემდეგ (1861). კანონიკური ფორმით წრფის განტოლება სივრცეში შემოიღო ო. კოშიმ. | + | პირველად [[ფერმა პიერ|პ. ფერმამ]] (1636) გამოთქვა შენიშვნა, რომ ნებისმიერი პირველი [[ხარისხი (მათემატიკა)|ხარისხის]] ორი ცვლადის განტოლება არის წრფის განტოლება. ამ ფაქტის დამტკიცება მოგვცა ი. დე ვიტომ (1658-1659). წრფის ნორმალური განტოლება ო. კოშისთან გვხვდება, მაგრამ საყოველთაო ხმარებაში შემოვიდა ო. გესეს [[გეომეტრია|გეომეტრიის]] სახელმძღვანელოს გამოსვლის შემდეგ (1861). კანონიკური ფორმით წრფის განტოლება [[სივრცე (მათემატიკა)|სივრცეში]] შემოიღო ო. კოშიმ. |
17:35, 3 ოქტომბერი 2023-ის ვერსია
წრფის განტოლება სხვადასხვა სახით დეკარტის კოორდინატებში ს ი ბ რ ტ ყ ე ზ ე.
1) ზოგადი სახის. Ax+By+C=0. (1)
A და B ერთდროულად არ უდრიან ნულს.
2) საკუთხო კოეფიციენტით. წრფე ადგენს φ კუთხეს 0x ღერძის დადებით მიმართულებასთან და კვეთს 0y ღერძს (0,b) წერტილში.
- y = kx + b, k = tgφ. (2)
k -ს ეწოდება საკუთხო კოეფიციენტი.
3) ღერძთა მონაკვეთებში. წრფე კვეთს Ox ღერძს (a,0) წერტილში და 0y ღერძს (0,b) წერტილში:
(a≠0, b≠0). (3)
4) ნორმალური სახის განტოლება. x cos θ + y sinθ - p = 0, (4)
სადაც P – კოორდინატთა სათავიდან წრფეზე დაშვებული პერპენდიკულარის სიგრძეა, ხოლო θ – კუთხე 0x ღერძის დადებით მიმართულებასა და პერპენდიკულარს შორის.
ნორმალური სახის (4) განტოლება შეიძლება მიღებული იქნას ზოგადი სახის (1) განტოლებიდანაც, თუ მას გავამრავლებთ მაინტეგრებელ μ მამრავლზე
μ -ს და C-ს ნიშნები ურთიერთსაწინააღმდეგო აქვთ.
თუ წრფის განტოლება მოცემულია ზოგადი სახით, მაშინ არსებობს დამოკიდებულებები:
- (2)-ში: k = - A/B, φ = θ - π/2, როცა k>0; φ = θ + π/2, როცა k<0.
- (3)-ში: a = -C/A, b = -C/B;
- (4)-ში:
5) წრფეთა კონის განტოლება ცენტრით M(x0, y0) წერტილში:
- y - y0 = k (x - x0). (5)
6) მოცემულ ორ M1 (x1, y1) და M2 (x2, y2) წერტილზე გამავალი წრფის განტოლება:
(6)
7) მანძილი M0 (x0, y0) წერტილიდან Ax + By + C = 0 წრფემდე:
(7)
ხოლო (4) სახით მოცემულ x cos θ + y sinθ − p = 0 წრფემდე
- δ = x0 cos θ + y0 sinθ − p.
8) კუთხე ორ მოცემულ წრფეს შორის:
- ა) თუ წრფეთა განტოლებები მოცემულია (1) ფორმით, მაშინ
(8)
- ბ) თუ წრფეთა განტოლებები მოცემულია (2) ფორმით, მაშინ
9) ორი წრფე იკვეთება ერთ წერტილში, როცა
ან k1≠k2; (9)
10) ორი წრფის პარალელობის პირობა:
ან k1=k2; (10)
11) ორი წრფის ურთიერთპერპენდიკულარობის პირობა:
- A1A2 + B1B2 = 0, ან k1k2 = - 1. (11)
ს ი ვ რ ც ე შ ი
12) ზოგადი სახის: წრფე, როგორც ორი სიბრტყის თანაკვეთა:
13) მოცემულ ორ M1(x1, y1, z1) და M2 (x2, y2, z2) წერტილზე გამავალი წრფის განტოლება:
(13)
14) მოცემულ M1(x1, y1, z1) წერტილზე გამავალი და მიმმართველი 
(ℓ, m, n) ვექტორის პარალელური წრფის განტოლება:
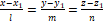(კანონიკური განტოლება), (14)
ან x = x1 + ℓt, y = y1 + mt, z = z1 + nt (პარამეტრული განტოლება).
15) კუთხე ორ მოცემულ წრფეს შორის:
თუ წრფეთა განტოლებები მოცემულია (14) ფორმით, მაშინ
(15)
16) ორი წრფის პარალელობის პირობა:
(16)
17) ორი წრფის ურთიერთპერპენდიკულარობის პირობა:
- l1l2 + m1m2 + n1n2 = 0. (17)
პირველად პ. ფერმამ (1636) გამოთქვა შენიშვნა, რომ ნებისმიერი პირველი ხარისხის ორი ცვლადის განტოლება არის წრფის განტოლება. ამ ფაქტის დამტკიცება მოგვცა ი. დე ვიტომ (1658-1659). წრფის ნორმალური განტოლება ო. კოშისთან გვხვდება, მაგრამ საყოველთაო ხმარებაში შემოვიდა ო. გესეს გეომეტრიის სახელმძღვანელოს გამოსვლის შემდეგ (1861). კანონიკური ფორმით წრფის განტოლება სივრცეში შემოიღო ო. კოშიმ.
