ლოქსოდრომი
(ახალი გვერდი: '''ლოქსოდრომი''' (''ბერძნ''. Λοξοζ – ირიბი, δρομοξ – სირბილი). ლოქსოდრომ...) |
|||
| (2 მომხმარებლების 2 შუალედური ვერსიები არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
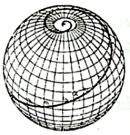
'''ლოქსოდრომი''' (''ბერძნ''. Λοξοζ – ირიბი, δρομοξ – სირბილი). ლოქსოდრომი – ირიბ მორბენალი – [[სფერო]]ზე ან რომელიმე [[ბრუნვითი ზედაპირი|ბრუნვით ზედაპირზე]] მდებარე [[წირი]], რომელიც ამ [[ზედაპირი (გეომეტრია)|ზედაპირის]] ყველა [[მერიდიანი|მერიდიანს]] კვეთს მუდმივი [[კუთხე (გეომეტრია)|კუთხით]]. | '''ლოქსოდრომი''' (''ბერძნ''. Λοξοζ – ირიბი, δρομοξ – სირბილი). ლოქსოდრომი – ირიბ მორბენალი – [[სფერო]]ზე ან რომელიმე [[ბრუნვითი ზედაპირი|ბრუნვით ზედაპირზე]] მდებარე [[წირი]], რომელიც ამ [[ზედაპირი (გეომეტრია)|ზედაპირის]] ყველა [[მერიდიანი|მერიდიანს]] კვეთს მუდმივი [[კუთხე (გეომეტრია)|კუთხით]]. | ||
| − | + | [[ფაილი:Loqsodromi.png|მარჯვნივ|130პქ]] | |
ლოქსოდრომის ფორმა აქვს ოკეანეში [[გემი]]ს ან დედამიწის ზედაპირისადმი [[თვითმფრინავი|თვითმფრინავის]] გზას მათი მუდმივი კურსით [[მოძრაობა|მოძრაობისას]]. | ლოქსოდრომის ფორმა აქვს ოკეანეში [[გემი]]ს ან დედამიწის ზედაპირისადმი [[თვითმფრინავი|თვითმფრინავის]] გზას მათი მუდმივი კურსით [[მოძრაობა|მოძრაობისას]]. | ||
[[ტერმინი]] შემოიღო ჰოლანდიელმა მეცნიერმა ვ. სნელიუსმა (1624). | [[ტერმინი]] შემოიღო ჰოლანდიელმა მეცნიერმა ვ. სნელიუსმა (1624). | ||
| − | თუ კუთხე α = 0 ან 180<sup>0</sup>, მაშინ ლოქსოდრომი ემთხვევა ბრუნვითი ზედაპირის მერიდიანს, თუ α=90<sup>0</sup>, ემთხვევა [[პარალელი|პარალელს]]. თუ α [[მახვილი კუთხე|მახვილი]]ა ან [[ბლაგვი კუთხე|ბლაგვი]], მაშინ ლოქსოდრომი [[პოლუსი | + | თუ კუთხე α = 0 ან 180<sup>0</sup>, მაშინ ლოქსოდრომი ემთხვევა ბრუნვითი ზედაპირის მერიდიანს, თუ α=90<sup>0</sup>, ემთხვევა [[პარალელი|პარალელს]]. თუ α [[მახვილი კუთხე|მახვილი]]ა ან [[ბლაგვი კუთხე|ბლაგვი]], მაშინ ლოქსოდრომი [[პოლუსი]]ს გარშემო ქმნის უსასრულო რაოდენობის ხვეულს და შემოუსაზღვრელად უახლოვდება მას. |
| + | ===== კარტოგრაფიასა და ნავიგაციაში ===== | ||
| + | კარტოგრაფიასა და ნავიგაციაში მიღებული ტერმინია. მისი განსაკუთრებულობა იმაში მდგომარეობს, რომ [[ეკვატორი]]დან პოლუსებისკენ სპირალურად მოძრავი სხეული ყველა მერიდიანს გადაკვეთს ერთი და იგივე კუთხით ([[აზიმუტი]]თ). ეკვატორი და პარალელები ლოქსოდრომებია. პრაქტიკული გამოყენება ჰპოვა [[მერკატორის პროექცია|მერკატორის ტოლკუთხა ცილინდრულ პროექცია]]ში, სადაც ლოქსოდრომი გამოისახება სწორი ხაზით, რომელიც ყველა მერიდიანთან ერთი და იგივე კუთხეს ქმნის და ამ კუთხით სვლისას გემი სასურველ პუნქტში ჩადის. | ||
| − | |||
| − | |||
| + | |||
| + | ==წყარო== | ||
| + | * [[მათემატიკის ენციკლოპედიური ლექსიკონი]] | ||
| + | * [[გეოგრაფიული კარტოგრაფიის ტერმინოლოგიური ცნობარი]] | ||
[[კატეგორია:მათემატიკა]] | [[კატეგორია:მათემატიკა]] | ||
| + | [[კატეგორია:კარტოგრაფიული ტერმინები]] | ||
მიმდინარე ცვლილება 22:33, 26 ნოემბერი 2024 მდგომარეობით
ლოქსოდრომი (ბერძნ. Λοξοζ – ირიბი, δρομοξ – სირბილი). ლოქსოდრომი – ირიბ მორბენალი – სფეროზე ან რომელიმე ბრუნვით ზედაპირზე მდებარე წირი, რომელიც ამ ზედაპირის ყველა მერიდიანს კვეთს მუდმივი კუთხით.
ლოქსოდრომის ფორმა აქვს ოკეანეში გემის ან დედამიწის ზედაპირისადმი თვითმფრინავის გზას მათი მუდმივი კურსით მოძრაობისას.
ტერმინი შემოიღო ჰოლანდიელმა მეცნიერმა ვ. სნელიუსმა (1624).
თუ კუთხე α = 0 ან 1800, მაშინ ლოქსოდრომი ემთხვევა ბრუნვითი ზედაპირის მერიდიანს, თუ α=900, ემთხვევა პარალელს. თუ α მახვილია ან ბლაგვი, მაშინ ლოქსოდრომი პოლუსის გარშემო ქმნის უსასრულო რაოდენობის ხვეულს და შემოუსაზღვრელად უახლოვდება მას.
[რედაქტირება] კარტოგრაფიასა და ნავიგაციაში
კარტოგრაფიასა და ნავიგაციაში მიღებული ტერმინია. მისი განსაკუთრებულობა იმაში მდგომარეობს, რომ ეკვატორიდან პოლუსებისკენ სპირალურად მოძრავი სხეული ყველა მერიდიანს გადაკვეთს ერთი და იგივე კუთხით (აზიმუტით). ეკვატორი და პარალელები ლოქსოდრომებია. პრაქტიკული გამოყენება ჰპოვა მერკატორის ტოლკუთხა ცილინდრულ პროექციაში, სადაც ლოქსოდრომი გამოისახება სწორი ხაზით, რომელიც ყველა მერიდიანთან ერთი და იგივე კუთხეს ქმნის და ამ კუთხით სვლისას გემი სასურველ პუნქტში ჩადის.