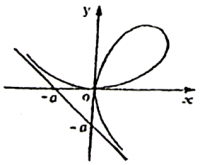
დეკარტის ფოთოლი
დეკარტის ფოთოლი – ბრტყელი წირი, რომლის განტოლებას დეკარტის მართკუთხა კოორდინატთა სისტემაში აქვს სახე: x3+y3-3axy=0. მისი ასიმპტოტი არის x+y+a=0 წრფე.
თუ დავუშვებთ, რომ y=xt, მივიღებთ დეკარტის ფოთოლის პარამეტრულ განტოლებას:
დეკარტის ფოთოლი სიმეტრიულია y=x ბისექტრისის მიმართ. საკვანძო წერტილია კოორდინატთა სათავეში x=0 და y=0 მხებებით. კოორდინატთა სისტემის სათავეში შტოების სიმრუდის რადიუსია R = ![]() a. ასიმპტოტი გადის წერტილებზე (-a, 0) და (0, -a). მარყუჟის ფართობია S1=
a. ასიმპტოტი გადის წერტილებზე (-a, 0) და (0, -a). მარყუჟის ფართობია S1=![]() a2. ფართობი წირსა და ასიმპტოტს შორის S2=
a2. ფართობი წირსა და ასიმპტოტს შორის S2=![]() a2.
a2.
დეკარტის ფოთოლი, როგორც გარკვეული თვისებების მქონე წირი, დეკარტიმ პირველად მოიხსენია ფერმასადმი გაგზავნილ წერილში (1638). წირის საბოლოო ფორმა მის ასიმპტოტთან ერთად განსაზღვრულია ჰიუგენსის და იოჰან ბერნულის მიერ (XVII ს-ის ბოლოს). დეკარტი იყენებდა სახელწოდებას „ფოთოლი“ (feuille). ჰიუგენსის წერილებში ლაიბნიცისადმი გვხვდება „დეკარტის ანუ რობერვალის ფოთოლი“. XVIII ს-ში დამკვიდრდა სახელწოდება „ფოთოლი“. ამასვე ადასტურებს დალამბერის სტატიაში გამოყენებული „დეკარტის ფოთოლი“.