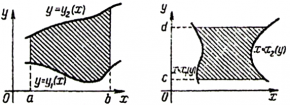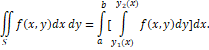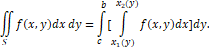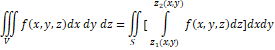ინტეგრალი ჯერადი
ინტეგრალი ჯერადი – ეს ცნება შემოღებულ იქნა XVIII საუკუნის შუა წლებში, დასაწყისში „განუსაზღვრელი ინტეგრალის სახით“.
ორჯერადი ინტეგრალი არის განსაზღვრული ინტეგრალი ორი ცვლადის ფუნქციიდან, რომელშიც ინტეგრება ხდება ორგანზომილებიან სიმრავლეზე;
თუ f(x,y) ფუნქცია 0xy სიბრტყის S არეში ღებულობს მხოლოდ დადებით მნიშვნელობებს, მაშინ ორჯერადი ინტეგრალი ასე ჩაიწერება:
f(x,y) ds, ან f(x,y) dx dy
და რიცხობრივად ტოლია ვერტიკალური 0z ღერძის პარალელური ცილინდრული სხეულისა, რომელიც 0xy სიბრტყეზე მდებარე S ფუძეზე არის აგებული და ზემოდან შემოსაზღვრულია z = f(x,y) ზედაპირის ნაწილით. S -ს ეწოდება ინტეგრების არე, ხოლო ds ან dxdy-ს – ამ არეს ფართობის ელემენტი.
0xy სიბრტყეზე მოთავსებულ ჩაკეტილ S არეზე f(x,y)=1 ფუნქციიდან ორჯერადი ინტეგრალი გამოსახავს S არეს ფართობს:
ორჯერადი ინტეგრალი შეიძლება გამოვთვალოთ თანმიმდევრობით ჩატარებული ორი მარტივი ინტეგრალის გამოთვლის შედეგად: თუ 0xy სიბრტყეზე S არე შემოსაზღვრულია წირებით: a ≤x≤ b, y1(x) ≤ y ≤ y2(x), მაშინ
ან თუ S: c ≤ y ≤ d, x1(y) ≤ x ≤ x2(y), მაშინ
ე. ი. x -ით ინტეგრების შედეგად ორჯერადი ინტეგრალი დაიყვანება ერთჯერად ინტეგრალზე.
სამჯერადი ინტეგრალი: ვთქვათ V არის სივრცითი სხეული, თუ მოცემულია V არეში განსაზღვრული შემოსაზღვრული f(x, y, z) ფუნქცია, მაშინ სამჯერადი ინტეგრალი f(x, y, z) ფუნქციიდან V არეზე ასე ჩაიწერება:
f(x,y,z)dv, ან f(x,y,z)dx dy dz
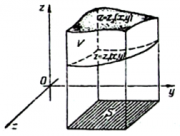
სამჯერადი ინტეგრალი შეიძლება დავიყვანოთ ორჯერად ინტეგრალზე. მაგალითად, თუ V არის ცილინდრული სხეული, რომელიც ქვემოდან შემოსაზღვრულია z = z1(x,y), ხოლო ზემოდან z = z2(x,y) ზედაპირებით, ამასთანავე V გეგმილი 0xy სიბრტყეზე არის S არე და მოცემულია V არეში განსაზღვრული შემოსაზღვრული f(x, y, z) ფუნქცია, მაშინ სამჯერადი ინტეგრალი f(x, y, z) ფუნქციიდან V არეზე ასე ჩაიწერება:
ე. ი. z -ით ინტეგრების შედეგად სამჯერადი ინტეგრალი დაიყვანება ორჯერად ინტეგრალზე.
1769 წელს ეილერმა დაადგინა ორჯერადი ინტეგრალის ცნება შემოსაზღვრულ არეზე და სხვადასხვა მაგალითზე აჩვენა, როგორ უნდა გამოვთვალოთ და გამოვიყენოთ ისინი. სამჯერადი ინტეგრალის ცნება შემოიღო ლაგრანჟმა (1770).
