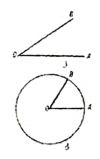კუთხე (გეომეტრია)
| (ერთი მომხმარებლის 2 შუალედური ვერსიები არ არის ნაჩვენები.) | |||
| ხაზი 1: | ხაზი 1: | ||
| − | '''კუთხე''' – [[სიბრტყე (გეომეტრია)|სიბრტყის]] ნაწილი, რომელიც შემოსაზღვრულია ერთი | + | '''კუთხე''' – [[სიბრტყე (გეომეტრია)|სიბრტყის]] ნაწილი, რომელიც შემოსაზღვრულია ერთი [[წერტილი (გეომეტრია)|წერტილი]]დან გამოსული ორი [[სხივი (გეომეტრია)|სხივი]]თ. ამ წერტილს ეწოდება კუთხის [[წვერო]], სხივებს - კუთხის გვერდები. |
[[ფაილი:Kutxe.PNG|მარჯვნივ|100პქ]] | [[ფაილი:Kutxe.PNG|მარჯვნივ|100პქ]] | ||
| − | კუთხე იზომება გრადუსებით ან რადიანებით. | + | კუთხე იზომება [[გრადუსი|გრადუსებით]] ან [[რადიანი|რადიანებით]]. |
კუთხე შეიძლება განვიხილოთ აგრეთვე როგორც: | კუთხე შეიძლება განვიხილოთ აგრეთვე როგორც: | ||
[[ფაილი:Kutxe1.PNG|მარჯვნივ|150პქ]] | [[ფაილი:Kutxe1.PNG|მარჯვნივ|150პქ]] | ||
| − | ა) ფიგურა, რომელიც მიიღება ფიქსირებული 0A სხივის მოცემულ 0B მდებარეობამდე ბრუნვით იმ 0 წერტილის გარშემო, საიდანაც გამოდის სხივი. ასეთი განსაზღვრა საშუალებას იძლევა განვაზოგადოთ კუთხის ცნება იმის მიხედვით, თუ რა მიმართულებით ხდება ბრუნვა. განასხვავებენ დადებითსა და უარყოფით კუთხეებს. | + | ა) [[ფიგურა (გეომეტრიული)|ფიგურა]], რომელიც მიიღება ფიქსირებული 0A სხივის მოცემულ 0B მდებარეობამდე [[ბრუნვა (მათემატიკა)|ბრუნვით]] იმ 0 წერტილის გარშემო, საიდანაც გამოდის სხივი. ასეთი განსაზღვრა საშუალებას იძლევა განვაზოგადოთ კუთხის ცნება იმის მიხედვით, თუ რა მიმართულებით ხდება ბრუნვა. განასხვავებენ დადებითსა და უარყოფით კუთხეებს. |
| − | ბ) ფიგურა – ცენტრალური | + | ბ) ფიგურა – [[ცენტრალური კუთხე]]ა; |
| − | გ) ფიგურა – 1 და 2, ასევე 3 და 4 – ვერტიკალური | + | გ) ფიგურა – 1 და 2, ასევე 3 და 4 – [[ვერტიკალური კუთხეები]]ა; |
| − | დ) ფიგურა – 1 და 2 მოსაზღვრე | + | დ) ფიგურა – 1 და 2 [[მოსაზღვრე კუთხეები]]ა; |
| − | ე) ფიგურა – ერთ წერტილში გადამკვეთ ორ წირს შორის კუთხეა. | + | ე) ფიგურა – ერთ წერტილში გადამკვეთ ორ [[წირი|წირს]] შორის კუთხეა. |
'''მრავალკუთხედის გარე კუთხე''' – ბრტყელი კუთხე, რომელიც წარმოიქმნება მრავალკუთხედის ორი მეზობელი გვერდის გაგრძელებით მიღებული სხივებით და მდებარეობს მრავალკუთხედის გარეთ. | '''მრავალკუთხედის გარე კუთხე''' – ბრტყელი კუთხე, რომელიც წარმოიქმნება მრავალკუთხედის ორი მეზობელი გვერდის გაგრძელებით მიღებული სხივებით და მდებარეობს მრავალკუთხედის გარეთ. | ||
| − | '''მრავალკუთხედის შიგა კუთხე''' – ბრტყელი კუთხე, წარმოქმნილი სხივებით, რომლებიც შეიცავენ | + | '''მრავალკუთხედის შიგა კუთხე''' – ბრტყელი კუთხე, წარმოქმნილი სხივებით, რომლებიც შეიცავენ [[მრავალკუთხედი]]ს ორი მეზობელ გვერდს და გააჩნია არაცარიელი [[თანაკვეთა]] მრავალკუთხედის შიგა [[არე]]სთან. |
| − | '''ორწახნაგა კუთხე''' – 1. გეომეტრიული ფიგურა, რომელიც წარმოქმნილია ერთი წრფიდან გამოსული ორი ნახევარსიბრტყით. 2. სივრცის ნაწილი, რომელიც შემოსაზღვრულია ერთი წრფიდან გამოსული ორი ნახევარსიბრტყით. | + | '''[[ორწახნაგა კუთხე]]''' – 1. [[გეომეტრიული ფიგურა]], რომელიც წარმოქმნილია ერთი [[წრფე|წრფიდან]] გამოსული ორი [[ნახევარსიბრტყე|ნახევარსიბრტყით]]. 2. [[სივრცე|სივრცის]] ნაწილი, რომელიც შემოსაზღვრულია ერთი წრფიდან გამოსული ორი ნახევარსიბრტყით. |
| − | '''კუთხე წრფესა და სიბრტყეს შორის''' ეწოდება კუთხეს, რომელსაც ადგენს წრფე და სიბრტყეზე ამ წრფის გეგმილი. | + | '''კუთხე წრფესა და სიბრტყეს შორის''' ეწოდება კუთხეს, რომელსაც ადგენს წრფე და სიბრტყეზე ამ წრფის [[გეგმილი (პროექცია)|გეგმილი]]. |
| − | '''წირებს შორის კუთხე''' – ზედაპირის ერთ წერტილში გადამკვეთ ორ წირს შორის კუთხე ეწოდება აღებულ წერტილში წირებისადმი გავლებულ მხებებს შორის ერთ-ერთ α კუთხეს. თუ ამ წირების პარამეტრული განტოლებებია შესაბამისად u=u<sub><small>1</small></sub>(t), v=v<sub><small>1</small></sub> (t), და u=u<sub><small>2</small></sub>(t), v=v<sub><small>2</small></sub>(t), მაშინ: | + | '''წირებს შორის კუთხე''' – [[ზედაპირი (გეომეტრია)|ზედაპირის]] ერთ წერტილში გადამკვეთ ორ წირს შორის კუთხე ეწოდება აღებულ წერტილში წირებისადმი გავლებულ [[მხები|მხებებს]] შორის ერთ-ერთ α კუთხეს. თუ ამ წირების [[პარამეტრი (მათემატიკა)|პარამეტრული]] [[განტოლება|განტოლებებია]] შესაბამისად u=u<sub><small>1</small></sub>(t), v=v<sub><small>1</small></sub> (t), და u=u<sub><small>2</small></sub>(t), v=v<sub><small>2</small></sub>(t), მაშინ: |
| ხაზი 29: | ხაზი 29: | ||
| − | სადაც E, F, G – ზედაპირის პირველი კვადრატული ფორმის კოეფიციენტებია, du<sub><small>k</small></sub> და dv<sub><small>k</small></sub> (k=1,2) – u და v-ს შესაბამისი დიფერენციალები; კერძოდ, საკოორდინატო კუთხეებისათვის, ანუ საკოორდინატო ბადის წირებს შორის კუთხისათვის, [[ფაილი:KuT009.png]] აქედან ჩანს, რომ საკოორდინატო წირები ადგენენ ორთოგონალურ ბადეს მაშინ და მხოლოდ მაშინ, როცა F = 0. | + | სადაც E, F, G – ზედაპირის პირველი [[კვადრატული ფორმა|კვადრატული ფორმის]] [[კოეფიციენტი (მათემატიკა)|კოეფიციენტებია]], du<sub><small>k</small></sub> და dv<sub><small>k</small></sub> (k=1,2) – u და v-ს შესაბამისი [[დიფერენციალი|დიფერენციალები]]; კერძოდ, საკოორდინატო კუთხეებისათვის, ანუ საკოორდინატო ბადის წირებს შორის კუთხისათვის, [[ფაილი:KuT009.png]] აქედან ჩანს, რომ საკოორდინატო წირები ადგენენ [[ორთოგონალურობა|ორთოგონალურ]] [[ბადე (მათემატიკა)|ბადეს]] მაშინ და მხოლოდ მაშინ, როცა F = 0. |
| − | კუთხის ცნება უძველესი დროიდან არის შემოღებული. ბერძნულ | + | კუთხის ცნება უძველესი დროიდან არის შემოღებული. ბერძნულ [[მათემატიკა]]ში იგი, ალბათ, გადავიდა ბაბილონელებისაგან, რომლებიც დახელოვნებულნი იყვნენ კუთხის გამოყენებაში თავიანთი დიდი [[ასტრონომია|ასტრონომიული]] გამოცდილების გამო. XVII საუკუნემდე ბერძენი და ყველა ევროპელი გეომეტრი იხილავდა მხოლოდ ორ [[მართი კუთხე|მართ კუთხეზე]] ([[გაშლილი კუთხე|გაშლილ კუთხეზე]]) ნაკლებ კუთხეს. მხოლოდ [[ეილერი ლეონარდ|ეილერმა]] შემოიღო კუთხის თანამედროვე ცნება (გაზომილი [[რადიანი|რადიანებში]]), რომელიც იღებს ნებისმიერ მნიშვნელობებს – დადებითს და უარყოფითს. |
| − | მართი კუთხე აღინიშნება d ასოთი, ფრანგული სიტყვიდან droit. კუთხის აღმნიშვნელი ∠ ნიშანი შემოიღო ერიგონმა (1634). ოტრედის | + | მართი კუთხე აღინიშნება d ასოთი, ფრანგული სიტყვიდან droit. კუთხის აღმნიშვნელი ∠ ნიშანი შემოიღო [[ერიგონი|ერიგონმა]] (1634). [[ოტრედი ვილიამი|ოტრედის]] „[[ტრიგონომეტრია]]ში“ (1657), ხოლო შემდგომ მრავალ სხვა ავტორთან ნიშანმა მიიღო თანამედროვე ∠ სახე. ერიგონმა ორი წრფის [[პერპენდიკულარი|პერპენდიკულარობა]] აღნიშნა ⊥ ნიშნით. a და b წრფეების მიერ შედგენილი კუთხის აღნიშვნა a^b ნიშნით პირველად გამოიყენეს ბინემ (1813), მებიუსმა (1827) და ფავარომ (1879). მართი კუთხის აღნიშვნა წერტილით (∟∙) შემოიღო ერნსტ მახმა (1906). |
მიმდინარე ცვლილება 01:53, 22 დეკემბერი 2023 მდგომარეობით
კუთხე – სიბრტყის ნაწილი, რომელიც შემოსაზღვრულია ერთი წერტილიდან გამოსული ორი სხივით. ამ წერტილს ეწოდება კუთხის წვერო, სხივებს - კუთხის გვერდები.
კუთხე იზომება გრადუსებით ან რადიანებით.
კუთხე შეიძლება განვიხილოთ აგრეთვე როგორც:
ა) ფიგურა, რომელიც მიიღება ფიქსირებული 0A სხივის მოცემულ 0B მდებარეობამდე ბრუნვით იმ 0 წერტილის გარშემო, საიდანაც გამოდის სხივი. ასეთი განსაზღვრა საშუალებას იძლევა განვაზოგადოთ კუთხის ცნება იმის მიხედვით, თუ რა მიმართულებით ხდება ბრუნვა. განასხვავებენ დადებითსა და უარყოფით კუთხეებს.
ბ) ფიგურა – ცენტრალური კუთხეა;
გ) ფიგურა – 1 და 2, ასევე 3 და 4 – ვერტიკალური კუთხეებია;
დ) ფიგურა – 1 და 2 მოსაზღვრე კუთხეებია;
ე) ფიგურა – ერთ წერტილში გადამკვეთ ორ წირს შორის კუთხეა.
მრავალკუთხედის გარე კუთხე – ბრტყელი კუთხე, რომელიც წარმოიქმნება მრავალკუთხედის ორი მეზობელი გვერდის გაგრძელებით მიღებული სხივებით და მდებარეობს მრავალკუთხედის გარეთ.
მრავალკუთხედის შიგა კუთხე – ბრტყელი კუთხე, წარმოქმნილი სხივებით, რომლებიც შეიცავენ მრავალკუთხედის ორი მეზობელ გვერდს და გააჩნია არაცარიელი თანაკვეთა მრავალკუთხედის შიგა არესთან.
ორწახნაგა კუთხე – 1. გეომეტრიული ფიგურა, რომელიც წარმოქმნილია ერთი წრფიდან გამოსული ორი ნახევარსიბრტყით. 2. სივრცის ნაწილი, რომელიც შემოსაზღვრულია ერთი წრფიდან გამოსული ორი ნახევარსიბრტყით.
კუთხე წრფესა და სიბრტყეს შორის ეწოდება კუთხეს, რომელსაც ადგენს წრფე და სიბრტყეზე ამ წრფის გეგმილი.
წირებს შორის კუთხე – ზედაპირის ერთ წერტილში გადამკვეთ ორ წირს შორის კუთხე ეწოდება აღებულ წერტილში წირებისადმი გავლებულ მხებებს შორის ერთ-ერთ α კუთხეს. თუ ამ წირების პარამეტრული განტოლებებია შესაბამისად u=u1(t), v=v1 (t), და u=u2(t), v=v2(t), მაშინ:
სადაც E, F, G – ზედაპირის პირველი კვადრატული ფორმის კოეფიციენტებია, duk და dvk (k=1,2) – u და v-ს შესაბამისი დიფერენციალები; კერძოდ, საკოორდინატო კუთხეებისათვის, ანუ საკოორდინატო ბადის წირებს შორის კუთხისათვის, ![]() აქედან ჩანს, რომ საკოორდინატო წირები ადგენენ ორთოგონალურ ბადეს მაშინ და მხოლოდ მაშინ, როცა F = 0.
აქედან ჩანს, რომ საკოორდინატო წირები ადგენენ ორთოგონალურ ბადეს მაშინ და მხოლოდ მაშინ, როცა F = 0.
კუთხის ცნება უძველესი დროიდან არის შემოღებული. ბერძნულ მათემატიკაში იგი, ალბათ, გადავიდა ბაბილონელებისაგან, რომლებიც დახელოვნებულნი იყვნენ კუთხის გამოყენებაში თავიანთი დიდი ასტრონომიული გამოცდილების გამო. XVII საუკუნემდე ბერძენი და ყველა ევროპელი გეომეტრი იხილავდა მხოლოდ ორ მართ კუთხეზე (გაშლილ კუთხეზე) ნაკლებ კუთხეს. მხოლოდ ეილერმა შემოიღო კუთხის თანამედროვე ცნება (გაზომილი რადიანებში), რომელიც იღებს ნებისმიერ მნიშვნელობებს – დადებითს და უარყოფითს.
მართი კუთხე აღინიშნება d ასოთი, ფრანგული სიტყვიდან droit. კუთხის აღმნიშვნელი ∠ ნიშანი შემოიღო ერიგონმა (1634). ოტრედის „ტრიგონომეტრიაში“ (1657), ხოლო შემდგომ მრავალ სხვა ავტორთან ნიშანმა მიიღო თანამედროვე ∠ სახე. ერიგონმა ორი წრფის პერპენდიკულარობა აღნიშნა ⊥ ნიშნით. a და b წრფეების მიერ შედგენილი კუთხის აღნიშვნა a^b ნიშნით პირველად გამოიყენეს ბინემ (1813), მებიუსმა (1827) და ფავარომ (1879). მართი კუთხის აღნიშვნა წერტილით (∟∙) შემოიღო ერნსტ მახმა (1906).