არქიმედეს სპირალი
მ (მომხმარებელმა Echelidze გვერდი „არქიმედეს ხვია“ გადაიტანა გვერდზე „არქიმედეს სპირალი“ გადამის...) |
|||
| ხაზი 1: | ხაზი 1: | ||
[[ფაილი:Arqimedes spirali.png|thumb|'''არქიმედეს სპირალი''']] | [[ფაილი:Arqimedes spirali.png|thumb|'''არქიმედეს სპირალი''']] | ||
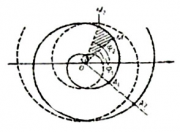
| − | '''[[არქიმედე]]ს სპირალი''' – ბრტყელი [[ტრანსცენდენტურობა|ტრანსცენდენტური]] მრუდი: M [[წერტილი (გეომეტრია)|წერტილის]] [[ტრაექტორია]], როდესაც იგი ასრულებს ორ [[თანაბარი მოძრაობა|თანაბარ მოძრაობას]]: 0 წერტილიდან მუდმივი v [[სიჩქარე|სიჩქარით]] [[მოძრაობა|მოძრაობს]] 0 [[პოლუსი | + | '''[[არქიმედე]]ს სპირალი''' – ბრტყელი [[ტრანსცენდენტურობა|ტრანსცენდენტური]] მრუდი: M [[წერტილი (გეომეტრია)|წერტილის]] [[ტრაექტორია]], როდესაც იგი ასრულებს ორ [[თანაბარი მოძრაობა|თანაბარ მოძრაობას]]: 0 წერტილიდან მუდმივი v [[სიჩქარე|სიჩქარით]] [[მოძრაობა|მოძრაობს]] 0 [[პოლუსი]]ს გარშემო მუდმივი ω [[კუთხე (გეომეტრია)|კუთხური]] სიჩქარით მბრუნავ OM [[სხივი (გეომეტრია)|სხივზე]]. [[კოორდინატები პოლარული|პოლარულ კოორდინატებში]] მისი [[განტოლება]]ა ρ = aφ (სადაც a = v/ω ≠0 მუდმივია); [[წირი]] შედგება ორი შტოსაგან (რომლებიც შეესაბამებიან φ-ს დადებით და უარყოფით მნიშვნელობებს). [[მანძილი (გეომეტრია)|მანძილი]] ორ [[მიმდევრობა (მათემატიკა)|მიმდევრობით]] [[ხვია (სპირალი)|ხვიას]] შორის მუდმივია; OA<sub><small>1</small></sub> = A<sub><small>1</small></sub> A<sub><small>2</small></sub> = 2πα. |
M<sub><small>1</small></sub> OM<sub><small>2</small></sub> [[სექტორი (მათემატიკა)|სექტორის]] [[ფართობი (გეომეტრია)|ფართობი]]: [[ფაილი:Arqimede1.PNG|120px]] | M<sub><small>1</small></sub> OM<sub><small>2</small></sub> [[სექტორი (მათემატიკა)|სექტორის]] [[ფართობი (გეომეტრია)|ფართობი]]: [[ფაილი:Arqimede1.PNG|120px]] | ||
მიმდინარე ცვლილება 22:30, 26 ნოემბერი 2024 მდგომარეობით
არქიმედეს სპირალი – ბრტყელი ტრანსცენდენტური მრუდი: M წერტილის ტრაექტორია, როდესაც იგი ასრულებს ორ თანაბარ მოძრაობას: 0 წერტილიდან მუდმივი v სიჩქარით მოძრაობს 0 პოლუსის გარშემო მუდმივი ω კუთხური სიჩქარით მბრუნავ OM სხივზე. პოლარულ კოორდინატებში მისი განტოლებაა ρ = aφ (სადაც a = v/ω ≠0 მუდმივია); წირი შედგება ორი შტოსაგან (რომლებიც შეესაბამებიან φ-ს დადებით და უარყოფით მნიშვნელობებს). მანძილი ორ მიმდევრობით ხვიას შორის მუდმივია; OA1 = A1 A2 = 2πα.
არქიმედეს სპირალი მიეკუთვნება ალგებრულ სპირალებს.
ზოგიერთი წყაროს მიხედვით, ამ სპირალის გამოგონება მიეწერება კონონს (III ს. ჩვ. წ.აღ-მდე), თუმცა მისი თვისებები შესწავლილი იყო არქიმედეს მიერ, რომელმაც განსაზღვრა მრუდისადმი მხებების აგება, შეასრულა მისი კვადრატურა. წირის განტოლება p=αφ ჩაწერილ იქნა XVII ს-ის ბოლოს. მაშინვე შეძლეს წირის გაწრფევება (კავალიერი, რობერვალი, ფერმა, პასკალი). ეილერმა პირველმა ააგო სპირალის მეორე შტო, რომელიც შეესაბამება რადიუს-ვექტორის უარყოფით მნიშვნელობებს. მაღალი რიგის არქიმედეს სპირალი pk=ak φ/2π ნახსენებია ფერმას მიერ მერსენისადმი მიწერილ წერილში (1636). როცა k=2, მიიღება წირი, რომელსაც ბერძნები „საოცარ წირს“ უწოდებდნენ. იგი, როგორც პაპი ირწმუნება, აღმოაჩინა ალექსანდრიელმა მენელეიმ. წირს იკვლევდა მრავალი მათემატიკოსი (ფერმა, ჰიუგენსი, ვალისი, დე სლიუზი (1633) და სხვ.).
არქიმედის სპირალი გამოიყენება ტექნიკაში. მაგალითად, გრამფირფიტაზე ბგერის ბილიკი წარმოადგენს არქიმედეს სპირალს: კორუნდიანი ნემსის წვერი ამ ბილიკზე გადაადგილდება ორი თანაბარი მოძრაობის შედეგად – პოლუსისკენ მიახლოებით და პოლუსის გარშემო ბრუნვით. საკერავი მანქანის ერთ-ერთ დეტალს – მასრაზე ძაფის თანაბარი დახვევის მექანიზმს აქვს არქიმედის სპირალის ფორმა.