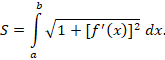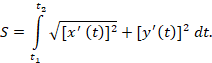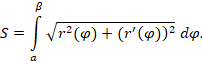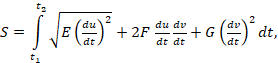რკალის სიგრძე

რკალის სიგრძე – ამ რკალში ჩახაზული ტეხილის პერიმეტრის ზღვარი, როდესაც ტეხილის შემადგენელი რგოლების რიცხვი უსაზღვროდ იზრდება, ხოლო თითოეული რგოლის სიგრძე მიისწრაფვის ნულისაკენ. უწყვეტი წირისათვის ასეთი ზღვარი სასრული ან უსასრულო ყოველთვის არსებობს. თუ ზღვარი სასრულია, წირს (რკალს) გაწრფევადი ეწოდება. წირის ანალიზური მოცემის ხერხის მიხედვით რკალის სიგრძე გამოითვლება შემდეგი ფორმულებით:

მართკუთხა კოორდინატებში მოცემული ბრტყელი უწყვეტი y = f(x) წირის სიგრძე (a ≤ x≤b) გამოისახება ინტეგრალით

თუ წირის განტოლება მოცემულია პარამეტრული სახით

x=x(t), y=y(t), t₁ ≤ t ≤ t₂,

მაშინ წირის სიგრძე

პოლარულ კოორდინატებში r = r(φ), φϵ [a,β ]

სივრცითი წირისათვის x=x(t), y=y(t), z=z(t), t₁ ≤ t ≤ t₂,

თუ წირი აღებულია = (u,v) ზედაპირზე და წირის შინაგანი განტოლებაა u=u(t), v=v(t), მაშინ ამ წირის რკალის სიგრძე გამოითვლება ფორმულით:

სადაც, t₁, t₂ – პარამეტრების მნიშვნელობებია, რომლებიც შეესაბამებიან წირის რკალის შემომსაზღვრელ წერტილებს. აქ მიღებულია დაშვება, რომ ზედაპირის პირველი ძირითადი კვადრატული ფორმის E, G, F კოეფიციენტების ფორმულებში u და v გამოსახულია t -ს საშუალებით.

წყარო

მათემატიკის ენციკლოპედიური ლექსიკონი